
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 3: Equations for Functions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
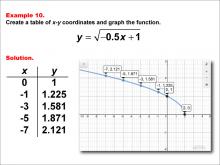
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 10 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 10TopicRadical Functions |
Radical Functions and Equations |
|
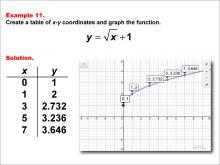
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 11 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 11TopicRadical Functions |
Radical Functions and Equations |
|
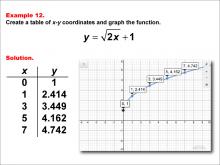
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 12 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 12TopicRadical Functions |
Radical Functions and Equations |
|
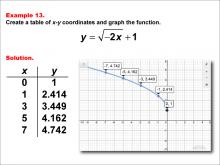
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 13 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 13TopicRadical Functions |
Radical Functions and Equations |
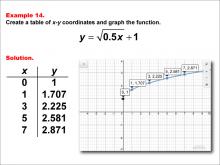
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 14 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 14TopicRadical Functions |
Radical Functions and Equations |
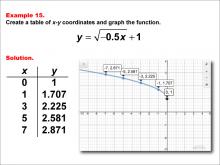
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 15 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 15TopicRadical Functions |
Radical Functions and Equations |
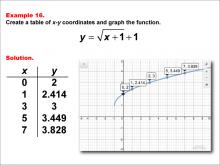
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 16 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 16TopicRadical Functions |
Radical Functions and Equations |
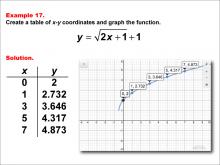
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 17 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 17TopicRadical Functions |
Radical Functions and Equations |
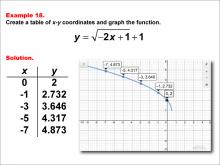
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 18 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 18TopicRadical Functions |
Radical Functions and Equations |
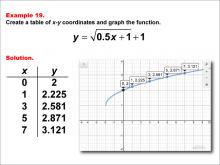
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 19 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 19TopicRadical Functions |
Radical Functions and Equations |
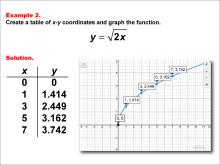
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 2 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 2TopicRadical Functions |
Radical Functions and Equations |
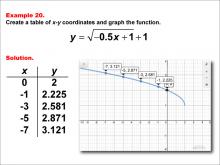
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 20 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 20TopicRadical Functions |
Radical Functions and Equations |
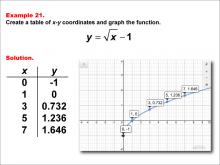
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 21 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 21TopicRadical Functions |
Radical Functions and Equations |
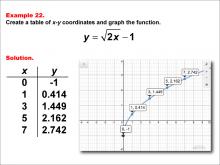
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 22 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 22TopicRadical Functions |
Radical Functions and Equations |
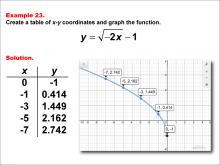
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 23 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 23TopicRadical Functions |
Radical Functions and Equations |
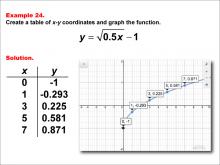
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 24 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 24TopicRadical Functions |
Radical Functions and Equations |
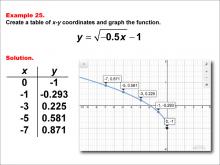
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 25 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 25TopicRadical Functions |
Radical Functions and Equations |
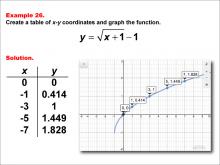
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 26 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 26TopicRadical Functions |
Radical Functions and Equations |
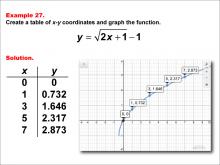
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 27 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 27TopicRadical Functions |
Radical Functions and Equations |
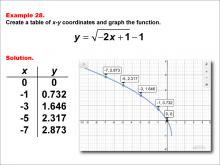
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 28 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 28TopicRadical Functions |
Radical Functions and Equations |
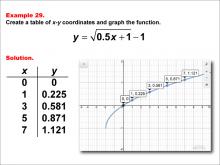
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 29 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 29TopicRadical Functions |
Radical Functions and Equations |
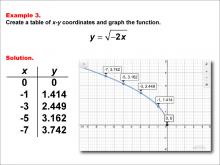
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 3 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 3TopicRadical Functions |
Radical Functions and Equations |
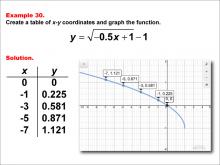
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 30 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 30TopicRadical Functions |
Radical Functions and Equations |
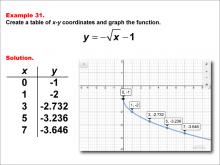
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 31 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 31TopicRadical Functions |
Radical Functions and Equations |
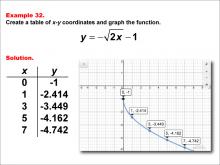
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 32 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 32TopicRadical Functions |
Radical Functions and Equations |
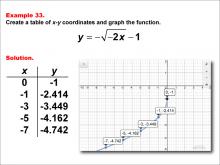
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 33 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 33TopicRadical Functions |
Radical Functions and Equations |
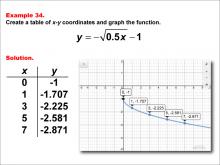
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 34 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 34TopicRadical Functions |
Radical Functions and Equations |
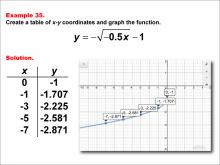
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 35 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 35TopicRadical Functions |
Radical Functions and Equations |
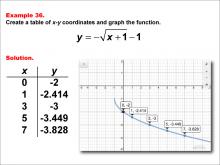
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 36 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 36TopicRadical Functions |
Radical Functions and Equations |
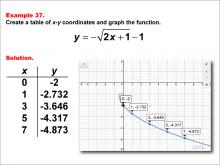
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 37 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 37TopicRadical Functions |
Radical Functions and Equations |
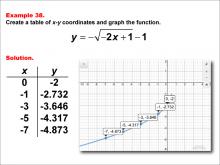
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 38 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 38TopicRadical Functions |
Radical Functions and Equations |
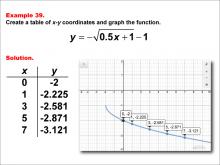
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 39 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 39TopicRadical Functions |
Radical Functions and Equations |
|
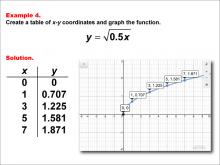
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 4 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 4TopicRadical Functions |
Radical Functions and Equations |
|
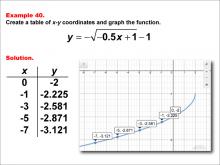
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 40 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 40TopicRadical Functions |
Radical Functions and Equations |
|
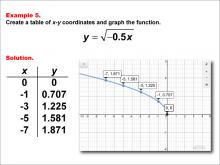
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 5 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 5TopicRadical Functions |
Radical Functions and Equations |
|
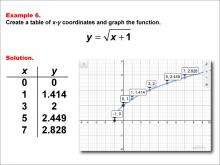
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 6 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 6TopicRadical Functions |
Radical Functions and Equations |
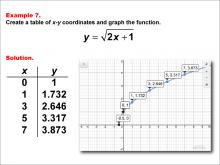
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 7 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 7TopicRadical Functions |
Radical Functions and Equations |
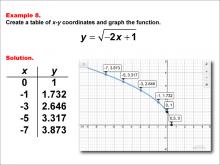
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 8 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 8TopicRadical Functions |
Radical Functions and Equations |
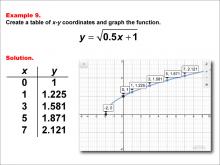
|
Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 9 | Math Example--Special Functions--Square Root Functions in Tabular and Graph Form: Example 9TopicRadical Functions |
Radical Functions and Equations |
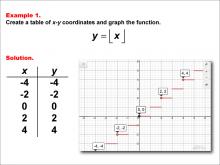
|
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 1 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 1TopicSpecial Functions |
Special Functions |
|
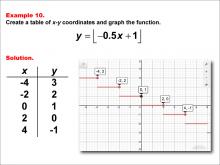
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 10 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 10TopicSpecial Functions DescriptionThis example presents a step function defined by y = floor(-0.5x + 1). The graph shows horizontal segments stepping down as x increases. The table contains x values (-4, -2, 0, 2, 4) and their corresponding y values (3, 2, 1, 0, -1), illustrating how the function behaves at these specific points. |
Special Functions |
|
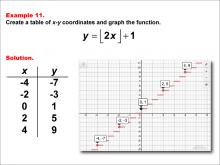
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 11 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 11TopicSpecial Functions DescriptionThis example illustrates a step function defined by y = floor(2x) + 1. The table shows x values (-4, -2, 0, 2, 4) and their corresponding y values (-7, -3, 1, 5, 9). The graph displays horizontal steps increasing as x increases, demonstrating how the function behaves across different intervals. |
Special Functions |
|
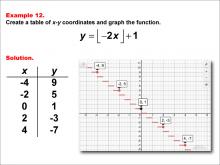
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 12 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 12TopicSpecial Functions DescriptionThis example demonstrates a step function defined by y = floor(-2x) + 1. The table shows x values (-4, -2, 0, 2, 4) and their corresponding y values (9, 5, 1, -3, -7). The graph displays horizontal line segments stepping down as x increases, illustrating how the function behaves across different intervals. |
Special Functions |
|
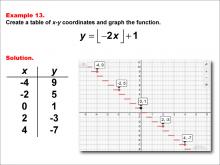
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 13 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 13TopicSpecial Functions DescriptionThis example showcases a step function defined by y = floor(-2x) + 1. The graph features red horizontal segments and black points at key coordinates, with x values of -4, -2, 0, 2, and 4, and corresponding y values of 9, 5, 1, -3, and -7. This visual representation helps students understand how the function behaves across different intervals. |
Special Functions |
|
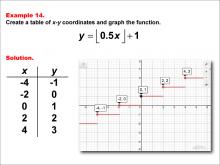
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 14 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 14TopicSpecial Functions DescriptionThis example illustrates a step function defined by y = floor(0.5x) + 1. The graph features red horizontal segments and black points at key coordinates, with x values of -4, -2, 0, 2, and 4, and corresponding y values of -1, 0, 1, 2, and 3. This visual representation helps students understand how the function behaves when the coefficient of x is a fraction. |
Special Functions |
|
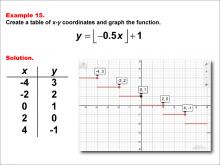
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 15 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 15TopicSpecial Functions DescriptionThis example demonstrates a step function defined by y = floor(-0.5x) + 1. The graph features red horizontal segments and black points at key coordinates, with x values of -4, -2, 0, 2, and 4, and corresponding y values of 3, 2, 1, 0, and -1. This visual representation helps students understand how the function behaves when the coefficient of x is a negative fraction. |
Special Functions |
|
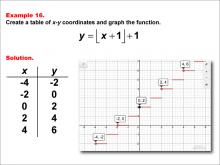
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 16 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 16TopicSpecial Functions DescriptionThis example illustrates a step function defined by y = floor(x + 1) + 1. The graph features red horizontal segments and black points at key coordinates, with x values of -4, -2, 0, 2, and 4, and corresponding y values of -2, 0, 2, 4, and 6. This visual representation helps students understand how the function behaves across different intervals. |
Special Functions |
|
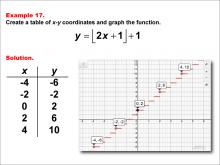
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 17 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 17TopicSpecial Functions DescriptionThis example demonstrates a step function defined by y = floor(2x + 1) + 1. The graph is plotted with points (-4, -6), (-2, -2), (0, 2), (2, 6), and (4, 10), showing horizontal steps that increase as x increases. This visual representation helps students understand how the function behaves when there's a coefficient greater than 1 inside the floor function. |
Special Functions |
|
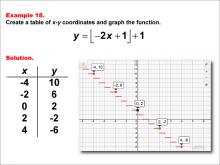
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 18 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 18TopicSpecial Functions DescriptionThis example showcases a step function defined by y = floor(-2x + 1) + 1. The graph consists of horizontal steps decreasing sharply as x increases, with points plotted at (-4, 10), (-2, 6), (0, 2), (2, -2), and (4, -6). This visual representation helps students understand how the function behaves when there's a negative coefficient inside the floor function. |
Special Functions |
|
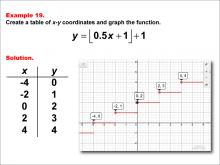
Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 19 | Math Example--Special Functions--Step Functions in Tabular and Graph Form: Example 19TopicSpecial Functions DescriptionThis example illustrates a step function defined by y = floor(0.5x + 1) + 1. The graph consists of horizontal steps increasing gradually as x increases, with points plotted at (-4, 0), (-2, 1), (0, 2), (2, 3), and (4, 4). This visual representation helps students understand how the function behaves when there's a fractional coefficient inside the floor function. |
Special Functions |