
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 7: Reasoning about Solving Equations (Part 1)
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
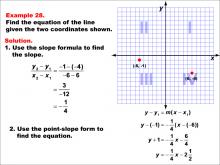
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |
|
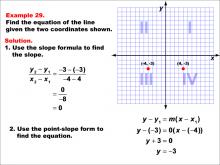
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 29TopicLinear Functions |
Point-Slope Form and Slope-Intercept Form |
|
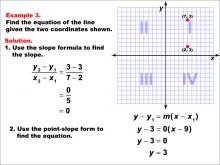
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 3TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a horizontal line passing through the points (2, 3) and (7, 3). The slope is calculated as 0 since both y-coordinates are the same. Using the point-slope form, y - y1 = m(x - x1), the equation becomes y - 3 = 0(x - any x-value), which simplifies to y = 3, representing a horizontal line. |
Point-Slope Form and Slope-Intercept Form |
|
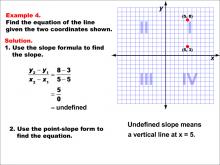
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 4TopicLinear Functions DescriptionThis example illustrates how to find the equation of a vertical line passing through the points (5, 3) and (5, 8). The slope is undefined because both x-coordinates are the same, resulting in division by zero when using the slope formula. This indicates a vertical line, and the equation is simply x = 5. |
Point-Slope Form and Slope-Intercept Form |
|
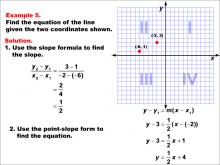
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 5TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a line passing through the points (-6, 1) and (-2, 3). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 1/2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived and simplified to y = (1/2)x + 4. |
Point-Slope Form and Slope-Intercept Form |
|
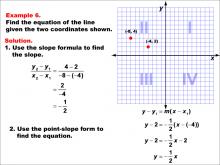
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 6TopicLinear Functions DescriptionThis image shows a graph with two points (-8, 4) and (-4, 2). The slope is calculated as (y2 - y1) / (x2 - x1), resulting in a slope of -1/2. The equation of the line is derived using point-slope form and simplified to y = -(1/2)x. The slope is calculated as -1/2, and the line equation is determined using point-slope form: y = -(1/2)x. |
Point-Slope Form and Slope-Intercept Form |
|
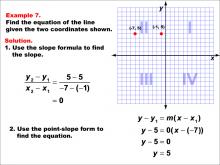
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 7TopicLinear Functions DescriptionThis image shows a graph with two points (-7, 5) and (-1, 5). The slope is calculated as zero since the y-values are equal. The equation of the line is horizontal, simplified to y = 5. The slope is 0, indicating a horizontal line. The equation is y = 5. |
Point-Slope Form and Slope-Intercept Form |
|
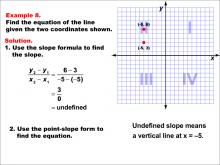
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 8TopicLinear Functions DescriptionThis image shows a graph with two points (-5, 6) and (-5, 3). The slope is undefined because the x-values are equal. This results in a vertical line at x = -5. The slope is undefined, indicating a vertical line at x = -5. |
Point-Slope Form and Slope-Intercept Form |
|
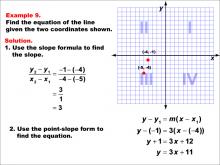
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 9TopicLinear Functions DescriptionThe image shows a coordinate plane with two points (-5, -4) and (-4, -1) marked. It provides a step-by-step solution to find the equation of the line passing through these points. The slope is calculated, and the equation is derived using point-slope form. The slope is calculated as (y2 - y1) / (x2 - x1) = (-1 - (-4)) / (-4 - (-5)) = 3 / 1 = 3. Using point-slope form, y - y1 = m(x - x1), the equation is derived as y + 1 = 3(x + 4), which simplifies to y = 3x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Percents--Equations with Percents: Example 1 | Math Example--Percents--Equations with Percents: Example 1TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 5% of 8?" The solution involves converting 5% to its decimal form, 0.05, and then multiplying it by 8 to get the result of 0.4. This straightforward approach demonstrates how to tackle basic percent calculations efficiently. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 10 | Math Example--Percents--Equations with Percents: Example 10TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 170% of 9.5?" The solution involves converting 170% to its decimal equivalent, 1.7, and then multiplying it by 9.5 to obtain the result of 16.15. This example combines a percentage greater than 100% with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 11 | Math Example--Percents--Equations with Percents: Example 11TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 225.5% of 78?" The solution involves converting 225.5% to its decimal form, 2.255, and then multiplying it by 78 to arrive at the answer of 175.89. This example introduces a decimal percentage greater than 200% and a larger whole number as the base value, demonstrating the scalability and flexibility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 12 | Math Example--Percents--Equations with Percents: Example 12TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 400% of 92.8?" The solution involves converting 400% to its decimal equivalent, 4.0, and then multiplying it by 92.8 to obtain the result of 371.2. This example showcases how to handle percentages greater than 100% and their application to decimal numbers, illustrating the versatility of the percent-to-decimal conversion method in complex scenarios. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 13 | Math Example--Percents--Equations with Percents: Example 13TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "5 is what percent of 9?" The solution involves setting up the equation 9 * (x / 100) = 5, then solving for x to get x = 5 * (100 / 9), which is approximately 55.56%. This example introduces a new type of percent problem where students must find the percentage given two known values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 14 | Math Example--Percents--Equations with Percents: Example 14TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "6 is what percent of 2.3?" The solution involves setting up the equation 2.3 * (x / 100) = 6, then solving for x to get x = 6 * (100 / 2.3), which is approximately 260.87%. This example introduces a scenario where the resulting percentage is greater than 100% and involves a decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 15 | Math Example--Percents--Equations with Percents: Example 15TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is what percent of 38?" The solution involves setting up the equation 38 * (x / 100) = 9, then solving for x to get x = 9 * (100 / 38), which is approximately 23.68%. This example demonstrates how to calculate a percentage when the first number is smaller than the second, resulting in a percentage less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 16 | Math Example--Percents--Equations with Percents: Example 16TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "2 is what percent of 55.5?" The solution involves setting up the equation 55.5 * (x / 100) = 2, then solving for x to get x = 2 * (100 / 55.5), which is approximately 3.6036%. This example introduces a scenario where the resulting percentage is a small fraction, less than 5%, and involves a decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 17 | Math Example--Percents--Equations with Percents: Example 17TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "8 is what percent of 120?" The solution involves setting up the equation 120 * (x / 100) = 8, then solving for x to get x = 8 * (100 / 120), which is approximately 6.67%. This example demonstrates how to calculate a percentage when dealing with larger whole numbers, resulting in a percentage less than 10%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 18 | Math Example--Percents--Equations with Percents: Example 18TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "3.5 is what percent of 350?" The solution involves setting up the equation 350 * (x / 100) = 3.5, then solving for x to get x = 3.5 * (100 / 350), which equals 1%. This example introduces a scenario where the resulting percentage is a whole number (1%) and involves a decimal number as the first value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 19 | Math Example--Percents--Equations with Percents: Example 19TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "12 is what percent of 8?" The solution involves setting up the equation 8 * (x / 100) = 12, then solving for x to get x = 12 * (100 / 8), which equals 150%. This example demonstrates how to calculate a percentage when the first number is larger than the second, resulting in a percentage greater than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 2 | Math Example--Percents--Equations with Percents: Example 2TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 7% of 9.5?" The solution involves converting 7% to its decimal equivalent, 0.07, and then multiplying it by 9.5 to obtain the result of 0.665. This example builds upon the previous one by introducing a decimal number as the base value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 20 | Math Example--Percents--Equations with Percents: Example 20TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "32 is what percent of 1.5?" The solution involves setting up the equation 1.5 * (x / 100) = 32, then solving for x to get x = 32 * (100 / 1.5), which equals 2133.3%. This example introduces a scenario where the resulting percentage is significantly larger than 100% and involves a decimal base number less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 21 | Math Example--Percents--Equations with Percents: Example 21TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "48 is what percent of 55?" The solution involves setting up the equation 55 * (x / 100) = 48, then solving for x to get x = 48 * (100 / 55), which equals 87.27%. This example demonstrates how to calculate a percentage when the two numbers are relatively close in value, resulting in a percentage close to but less than 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 22 | Math Example--Percents--Equations with Percents: Example 22TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "52.2 is what percent of 98.5?" The solution involves setting up the equation 98.5 * (x / 100) = 52.2, then solving for x to get x = 52.2 * (100 / 98.5), which is approximately 52.99%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that is also close to the original numerator. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 23 | Math Example--Percents--Equations with Percents: Example 23TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "68 is what percent of 320?" The solution involves setting up the equation 320 * (x / 100) = 68, then solving for x to get x = 68 * (100 / 320), which equals 21.25%. This example demonstrates how to calculate a percentage when dealing with whole numbers, resulting in a percentage that's less than 25%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 24 | Math Example--Percents--Equations with Percents: Example 24TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "75.5 is what percent of 555.25?" The solution involves setting up the equation 555.25 * (x / 100) = 75.5, then solving for x to get x = 75.5 * (100 / 555.25), which is approximately 13.59%. This example introduces a scenario where both the numerator and denominator are decimal numbers, resulting in a percentage that's less than 15%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 25 | Math Example--Percents--Equations with Percents: Example 25TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "125 is what percent of 2?" The solution involves setting up the equation 2 * (x / 100) = 125, then solving for x to get x = 125 * (100 / 2), which equals 6250%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage well over 100%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 26 | Math Example--Percents--Equations with Percents: Example 26TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 3.5?" The solution involves setting up the equation 3.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 3.5), which equals 8571.43%. This example introduces a scenario where the resulting percentage is extremely large, over 8000%, due to the first number being significantly larger than the small decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 27 | Math Example--Percents--Equations with Percents: Example 27TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "278 is what percent of 99?" The solution involves setting up the equation 99 * (x / 100) = 278, then solving for x to get x = 278 * (100 / 99), which equals 280.80%. This example demonstrates how to calculate a percentage when the first number is significantly larger than the second, resulting in a percentage greater than 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 28 | Math Example--Percents--Equations with Percents: Example 28TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "300 is what percent of 75.5?" The solution involves setting up the equation 75.5 * (x / 100) = 300, then solving for x to get x = 300 * (100 / 75.5), which equals 397.35%. This example introduces a scenario where the resulting percentage is close to 400%, with the first number being significantly larger than the decimal base number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 29 | Math Example--Percents--Equations with Percents: Example 29TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is what percent of 220?" The solution involves setting up the equation 220 * (x / 100) = 400, then solving for x to get x = 400 * (100 / 220), which equals 181.81%. This example demonstrates how to calculate a percentage when the first number is nearly double the second, resulting in a percentage between 150% and 200%. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 3 | Math Example--Percents--Equations with Percents: Example 3TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 8% of 58?" The solution involves converting 8% to its decimal form, 0.08, and then multiplying it by 58 to arrive at the answer of 4.64. This example introduces a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 30 | Math Example--Percents--Equations with Percents: Example 30TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "333.5 is what percent of 500.25?" The solution involves setting up the equation 500.25 * (x / 100) = 333.5, then solving for x to get x = 333.5 * (100 / 500.25), which is approximately 66.67%. This example introduces a scenario where both numbers are decimals and the resulting percentage is less than 100%, showing how to handle more complex decimal calculations. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 31 | Math Example--Percents--Equations with Percents: Example 31TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "4 is 0.1% of what number?" The solution involves setting up the equation 4 = 0.001 * x, then solving for x to get x = 4 / 0.001, which equals 4000. This example demonstrates how to calculate the whole when given a very small percentage of it, resulting in a much larger number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 32 | Math Example--Percents--Equations with Percents: Example 32TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "7 is 1% of what number?" The solution involves setting up the equation 7 = 0.01 * x, then solving for x to get x = 7 / 0.01, which equals 700. This example introduces a scenario where we need to find the whole when given a small percentage of it, resulting in a number 100 times larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 33 | Math Example--Percents--Equations with Percents: Example 33TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is 30% of what number?" The solution involves setting up the equation 9 = 0.3 * x, then solving for x to get x = 9 / 0.3, which equals 30. This example demonstrates how to calculate the whole when given a larger percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 34 | Math Example--Percents--Equations with Percents: Example 34TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "1 is 400% of what number?" The solution involves setting up the equation 1 = 4.0 * x, then solving for x to get x = 1 / 4, which equals 0.25. This example introduces a scenario where we need to find a number that, when increased by 400%, results in 1, leading to a fraction or decimal less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 35 | Math Example--Percents--Equations with Percents: Example 35TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "15 is 0.25% of what number?" The solution involves setting up the equation 15 = 0.0025 * x, then solving for x to get x = 15 / 0.0025, which equals 6000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 36 | Math Example--Percents--Equations with Percents: Example 36TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "30 is 5% of what number?" The solution involves setting up the equation 30 = 0.05 * x, then solving for x to get x = 30 / 0.05, which equals 600. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a much larger number. |
Solving Percent Equations |
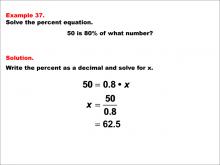
|
Math Example--Percents--Equations with Percents: Example 37 | Math Example--Percents--Equations with Percents: Example 37TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "50 is 80% of what number?" The solution involves setting up the equation 50 = 0.8 * x, then solving for x to get x = 50 / 0.8, which equals 62.5. This example introduces a scenario where we need to find the whole when given a large percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
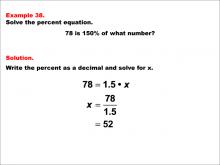
|
Math Example--Percents--Equations with Percents: Example 38 | Math Example--Percents--Equations with Percents: Example 38TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "78 is 150% of what number?" The solution involves setting up the equation 78 = 1.5 * x, then solving for x to get x = 78 / 1.5, which equals 52. This example demonstrates how to calculate the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
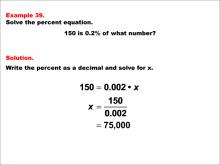
|
Math Example--Percents--Equations with Percents: Example 39 | Math Example--Percents--Equations with Percents: Example 39TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "150 is 0.2% of what number?" The solution involves setting up the equation 150 = 0.002 * x, then solving for x to get x = 150 / 0.002, which equals 75,000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 4 | Math Example--Percents--Equations with Percents: Example 4TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 6.5% of 45.5?" The solution involves converting 6.5% to its decimal equivalent, 0.065, and then multiplying it by 45.5 to obtain the result of 2.9575. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation. |
Solving Percent Equations |
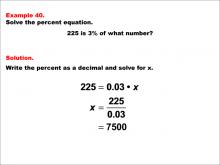
|
Math Example--Percents--Equations with Percents: Example 40 | Math Example--Percents--Equations with Percents: Example 40TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "225 is 3% of what number?" The solution involves setting up the equation 225 = 0.03 * x, then solving for x to get x = 225 / 0.03, which equals 7,500. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 41 | Math Example--Percents--Equations with Percents: Example 41TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is 40% of what number?" The solution involves setting up the equation 400 = 0.4 * x, then solving for x to get x = 400 / 0.4, which equals 1000. This example demonstrates how to calculate the whole when given a significant percentage of it, resulting in a number that is larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 42 | Math Example--Percents--Equations with Percents: Example 42TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "650 is 130% of what number?" The solution involves setting up the equation 650 = 1.3 * x, then solving for x to get x = 650 / 1.3, which equals 500. This example introduces a scenario where we need to find the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 5 | Math Example--Percents--Equations with Percents: Example 5TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 30% of 9?" The solution involves converting 30% to its decimal form, 0.3, and then multiplying it by 9 to get the result of 2.7. This example introduces a larger percentage, demonstrating how the method applies consistently across various percentage values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 6 | Math Example--Percents--Equations with Percents: Example 6TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 28% of 7.2?" The solution involves converting 28% to its decimal equivalent, 0.28, and then multiplying it by 7.2 to obtain the result of 2.016. This example combines a whole number percentage with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 7 | Math Example--Percents--Equations with Percents: Example 7TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 45% of 68?" The solution involves converting 45% to its decimal form, 0.45, and then multiplying it by 68 to arrive at the answer of 30.6. This example introduces a larger percentage and a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 8 | Math Example--Percents--Equations with Percents: Example 8TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 52.3% of 36.9?" The solution involves converting 52.3% to its decimal equivalent, 0.523, and then multiplying it by 36.9 to obtain the result of 19.2987. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation and showcasing the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |