
Illustrative Math Alignment: Grade 7 Unit 8
Probability and Sampling
Lesson 16: Estimating Population Proportions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
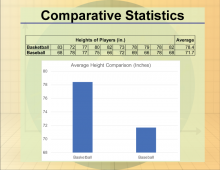
Math Clip Art--Statistics--Comparative Statistics--01 | Math Clip Art--Statistics--Comparative Statistics--01
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Analysis |
|
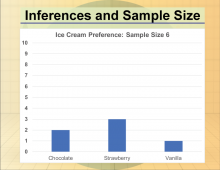
Math Clip Art--Statistics--Inferences and Sample Size--01 | Math Clip Art--Statistics--Inferences and Sample Size--01
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
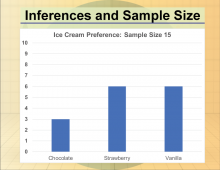
Math Clip Art--Statistics--Inferences and Sample Size--02 | Math Clip Art--Statistics--Inferences and Sample Size--02
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
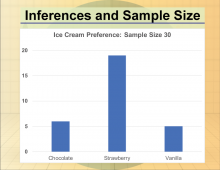
Math Clip Art--Statistics--Inferences and Sample Size--03 | Math Clip Art--Statistics--Inferences and Sample Size--03
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
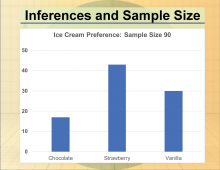
|
Math Clip Art--Statistics--Inferences and Sample Size--04 | Math Clip Art--Statistics--Inferences and Sample Size--04
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
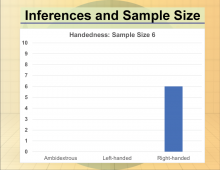
|
Math Clip Art--Statistics--Inferences and Sample Size--05 | Math Clip Art--Statistics--Inferences and Sample Size--05
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
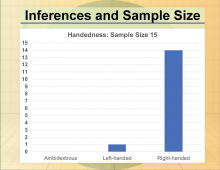
|
Math Clip Art--Statistics--Inferences and Sample Size--06 | Math Clip Art--Statistics--Inferences and Sample Size--06
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
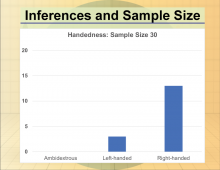
|
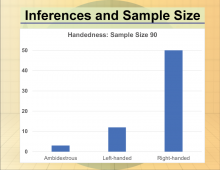
Math Clip Art--Statistics--Inferences and Sample Size--07 | Math Clip Art--Statistics--Inferences and Sample Size--07
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
Math Clip Art--Statistics--Inferences and Sample Size--08 | Math Clip Art--Statistics--Inferences and Sample Size--08
This is part of a collection of math clip art images that show different statistical graphs and concepts, along with some probability concepts. |
Data Gathering |
|
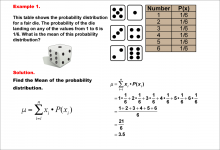
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 1 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for a probability distribution of a fair six-sided die. The probability of each outcome (1 to 6) is equally 1/6. The mean is calculated by multiplying each possible outcome by its probability and summing the results. For this fair die, the mean is determined to be 3.5. |
Data Analysis |
|
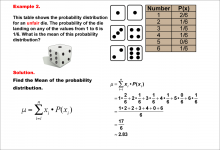
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 2 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 2TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for a probability distribution of an unfair six-sided die. Unlike a fair die, the probabilities are not equally distributed, with a higher probability (2/6) for rolling a 1. The mean is calculated using the same method as before, resulting in approximately 2.83. |
Data Analysis |
|
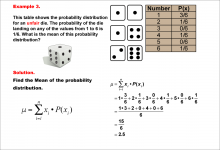
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 3 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 3TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for another unfair six-sided die. In this case, the probability of rolling a 1 is even higher (3/6), while some numbers have a probability of 0. The mean is calculated using the same method, resulting in 2.5. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 4 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 4TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for an unfair six-sided die where the number 5 has a significantly higher probability (3/6) than other numbers. The mean is calculated using the same method as previous examples, resulting in 4.5. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 5 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 5TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the probability distribution of the sum when rolling two fair dice. There are 11 possible outcomes (2 to 12), each with its own probability. The mean is calculated using the same method as previous examples, resulting in 7. |
Data Analysis |
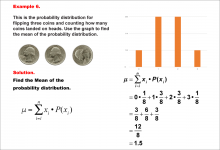
|
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 6 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 6TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the mean for the probability distribution of the number of heads when flipping three fair coins. The possible outcomes are 0, 1, 2, or 3 heads, each with its own probability. The mean is calculated using the same method as previous examples, resulting in 1.5. |
Data Analysis |
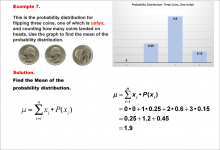
|
Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 7 | Math Example--Measures of Central Tendency--Mean of a Probability Distribution--Example 7TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the mean for the probability distribution of the number of heads when flipping three coins, one of which is unfair. The possible outcomes are 0, 1, 2, or 3 heads, but the probabilities are skewed due to the unfair coin. The mean is calculated using the same method as previous examples, resulting in 1.9. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 1 | Math Example--Measures of Central Tendency--Range: Example 1TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 10 | Math Example--Measures of Central Tendency--Range: Example 10TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: -33, 38, 29, -8, 12, 2, 36, -8, 12, 18, -23, 50. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 83. This example is particularly useful as it includes both positive and negative numbers, helping students understand how to handle different types of values when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 11 | Math Example--Measures of Central Tendency--Range: Example 11TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 16, 50, 24, 31, 30, 6, 22, 32, 43, 27, 48, 17, 36. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 44. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 12 | Math Example--Measures of Central Tendency--Range: Example 12TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 34, 5, 43, 24, -48, -31, -49, 8, -41, 5, 0, 20, -41. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 92. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 13 | Math Example--Measures of Central Tendency--Range: Example 13TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 50, 18, 47, 29, 33, 27, 23, 34, 43, 17, 10, 15, 22. The solution involves arranging the numbers from least to greatest (10 to 50) and finding the difference between the two extremes. The range is calculated to be 40. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 14 | Math Example--Measures of Central Tendency--Range: Example 14TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 0, 12, -41, -47, 7, -29, -34, -24, 38, 25, 23, -9, 38, 12. The solution involves arranging the numbers from least to greatest (-47 to 38) and finding the difference between the two extremes. The range is calculated to be 85. This example is particularly valuable as it includes a mix of positive, negative, and zero values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 15 | Math Example--Measures of Central Tendency--Range: Example 15TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 49, 20, 13, 40, 45, 14, 2, 27, 16, 48, 43, 39, 44, 26, 12. The solution involves arranging the numbers from least to greatest (2 to 49) and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of numbers and find their difference. |
Data Analysis |
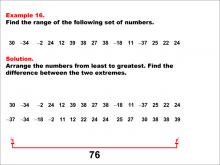
|
Math Example--Measures of Central Tendency--Range: Example 16 | Math Example--Measures of Central Tendency--Range: Example 16TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, -34, -2, 24, 12, 39, 38, 27, 38, -18, 11, -37, 25, 22, 24. The solution involves arranging the numbers from least to greatest (-37 to 39) and finding the difference between the two extremes. The range is calculated to be 76. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |
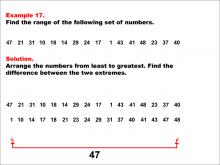
|
Math Example--Measures of Central Tendency--Range: Example 17 | Math Example--Measures of Central Tendency--Range: Example 17TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 47, 21, 31, 10, 18, 14, 29, 24, 17, 1, 43, 41, 48, 23, 37, 40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 47. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 18 | Math Example--Measures of Central Tendency--Range: Example 18TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: -2, -10, 24, -2, 26, 50, -40, 50, -40, 36, 30, -19, -40, 46, 27, -2. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 90. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 19 | Math Example--Measures of Central Tendency--Range: Example 19TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 14, 29, 44, 37, 9, 6, 41, 30, 19, 2, 38, 50, 26, 24, 40, 11, 45. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 2 | Math Example--Measures of Central Tendency--Range: Example 2TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 20 | Math Example--Measures of Central Tendency--Range: Example 20TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 30, 31, -27, 46, 25, 6, 41, 1, -27, 40, -8, -35, 9, -25, -25, -41, -38. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 87. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |
|
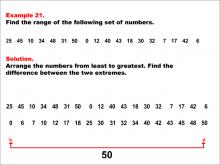
Math Example--Measures of Central Tendency--Range: Example 21 | Math Example--Measures of Central Tendency--Range: Example 21TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 25, 45, 10, 34, 48, 31, 50, 0, 12, 40, 43, 18, 30, 32, 7, 17, 42, 6. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 50. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
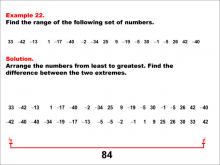
Math Example--Measures of Central Tendency--Range: Example 22 | Math Example--Measures of Central Tendency--Range: Example 22TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 33, -42, -13, 1, -17, -40, -2, -34, 25, 9, -19, -5, 30, -1, -5, 26, 42, -40. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 84. This example is particularly valuable as it includes a mix of positive and negative values, helping students understand how to handle diverse datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 23 | Math Example--Measures of Central Tendency--Range: Example 23TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 39, 28, 32, 33, 49, 46, 43, 17, 35, 11, 40, 31, 26, 1, 44, 37, 20, 15, 27. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of positive numbers and find their difference. |
Data Analysis |
|
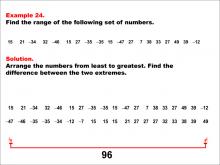
Math Example--Measures of Central Tendency--Range: Example 24 | Math Example--Measures of Central Tendency--Range: Example 24TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 15, 21, -34, 32, -46, 15, 27, -35, -35, 15, -47, 27, 7, 38, 33, 27, 49, 39, -12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 96. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 25 | Math Example--Measures of Central Tendency--Range: Example 25TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of the following set of numbers: 42, 31, 16, 0, 35, 26, 30, 14, 6, 2, 13, 37, 33, 36, 19, 48, 3, 9, 45, 12. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 48. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a larger set of non-negative numbers and find their difference. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 26 | Math Example--Measures of Central Tendency--Range: Example 26TopicMeasures of Central Tendency DescriptionThis example illustrates how to find the range of the following set of numbers: 28, 49, 1, -19, -37, 43, 27, 32, -10, 39, -19, -48, -49, 28, 36, 37, 44, 42, 29, -17. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 98. This example is particularly valuable as it includes a mix of positive and negative values, as well as repeated numbers, helping students understand how to handle diverse and complex datasets when calculating the range. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 3 | Math Example--Measures of Central Tendency--Range: Example 3TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 4 | Math Example--Measures of Central Tendency--Range: Example 4TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 5 | Math Example--Measures of Central Tendency--Range: Example 5TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 6 | Math Example--Measures of Central Tendency--Range: Example 6TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 7 | Math Example--Measures of Central Tendency--Range: Example 7TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 8 | Math Example--Measures of Central Tendency--Range: Example 8TopicMeasures of Central Tendency |
Data Analysis |

|
Math Example--Measures of Central Tendency--Range: Example 9 | Math Example--Measures of Central Tendency--Range: Example 9TopicMeasures of Central Tendency DescriptionThis example demonstrates how to find the range of a set of numbers: 22, 13, 15, 1, 16, 28, 3, 5, 18, 42, 8, 9. The solution involves arranging the numbers from least to greatest and finding the difference between the two extremes. The range is calculated to be 41. This example is valuable for understanding the concept of range, as it teaches students how to identify the maximum and minimum from a set of numbers and find their difference. The process encourages critical thinking and helps students visualize the relationship between numbers in a dataset. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 1 | Math Example--Measures of Central Tendency--Sample Mean--Example 1TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 trout. The image displays a table showing the lengths of these trout, along with the formula for calculating the sample mean. The population of adult trout has a mean length of 15 inches with a standard deviation of 2. The sample mean is calculated by summing all the lengths (472.22 inches) and dividing by the number of trout (30), resulting in a sample mean of 15.74 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 2 | Math Example--Measures of Central Tendency--Sample Mean--Example 2TopicMeasures of Central Tendency DescriptionThis example presents another calculation of the sample mean for a group of 30 trout. The image shows a table with the lengths of these trout and the formula for the sample mean. The population of adult trout has a mean length of 15 inches with a standard deviation of 2. The sample mean is computed by adding all the lengths (436.73 inches) and dividing by the number of trout (30), yielding a sample mean of 14.56 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 3 | Math Example--Measures of Central Tendency--Sample Mean--Example 3TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the sample mean for a group of 40 trout. The image displays a table showing the lengths of these trout, along with the formula for calculating the sample mean. The population of adult trout has a mean length of 15 inches with a standard deviation of 2. The sample mean is calculated by summing all the lengths (615.86 inches) and dividing by the number of trout (40), resulting in a sample mean of 15.39 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 4 | Math Example--Measures of Central Tendency--Sample Mean--Example 4TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 macaws. The image shows a table with the wingspans of these macaws and the formula for calculating the sample mean. The population of adult macaws has an average wingspan of 48 inches with a standard deviation of 6. The sample mean is computed by summing all the wingspans (1432.28 inches) and dividing by the number of macaws (30), yielding a sample mean of 47.74 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 5 | Math Example--Measures of Central Tendency--Sample Mean--Example 5TopicMeasures of Central Tendency DescriptionThis example illustrates the calculation of the sample mean for another group of 30 macaws. The image displays a table showing the wingspans of these macaws, along with the formula for calculating the sample mean. The population of adult macaws has an average wingspan of 48 inches with a standard deviation of 6. The sample mean is calculated by summing all the wingspans (1398.02 inches) and dividing by the number of macaws (30), resulting in a sample mean of 46.6 inches. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 6 | Math Example--Measures of Central Tendency--Sample Mean--Example 6TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 adult male elephants. The image shows a table with the weights of these elephants and the formula for calculating the sample mean. The population of adult male elephants has an average weight of 12,000 pounds with a standard deviation of 1,500 pounds. The sample mean is computed by summing all the weights (370,924.22 pounds) and dividing by the number of elephants (30), yielding a sample mean of 12,364.14 pounds. |
Data Analysis |

|
Math Example--Measures of Central Tendency--Sample Mean--Example 7 | Math Example--Measures of Central Tendency--Sample Mean--Example 7TopicMeasures of Central Tendency DescriptionThis example demonstrates the calculation of the sample mean for a group of 30 mature sequoia trees. The image presents a table showing the heights of these trees, along with the formula for computing the sample mean. The population of mature sequoia trees has an average height of 220 feet with a standard deviation of 25 feet. By summing all the heights (6,844.64 feet) and dividing by the number of trees (30), we obtain a sample mean of 228.15 feet. |
Data Analysis |

|
Math in the News: Issue 100--Late Night TV Ratings | Math in the News: Issue 100--Late Night TV Ratings
July 2014. In this issue of Math in the News we look at the mathematics of the Nielsen Ratings. This provides an excellent application of ratios, proportions, and percents. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Data Analysis |