
Illustrative Math Alignment: Grade 8 Unit 1
Rigid Transformations and Congruence
Lesson 17: Rotate and Tessellate
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
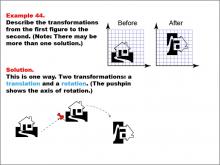
Math Example--Geometric Transformation--Transformations: Example 44 | Math Example--Geometric Transformation--Transformations: Example 44TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image shows two house icons on a grid, labeled "Before" and "After." Two transformations occur: translation (shown by an arrow) and rotation (shown by a pushpin). This demonstrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
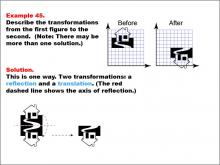
Math Example--Geometric Transformation--Transformations: Example 45 | Math Example--Geometric Transformation--Transformations: Example 45TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows two figures labeled as "Before" and "After." The left figure illustrates a shape on a grid, while the right figure shows the same shape after a transformation involving reflection and translation, marked with a dashed red line. This illustrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
Math Example--Geometric Transformation--Transformations: Example 46 | Math Example--Geometric Transformation--Transformations: Example 46TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image presents two figures labeled "Before" and "After." The left figure shows a shape on a grid, while the right one displays the same shape after a rotation around a specified point marked with a pushpin. This illustrates how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
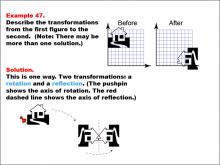
Math Example--Geometric Transformation--Transformations: Example 47 | Math Example--Geometric Transformation--Transformations: Example 47TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. Two figures are presented, labeled "Before" and "After." The left figure shows the original shape on a grid, while the right figure depicts the shape after undergoing a combination of transformations: first, a rotation around a point indicated by a pushpin, followed by a reflection across a dashed red line. |
Definition of Transformations |
|
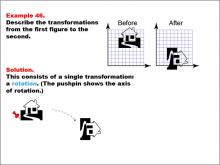
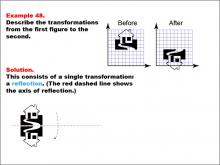
Math Example--Geometric Transformation--Transformations: Example 48 | Math Example--Geometric Transformation--Transformations: Example 48TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. The image shows two figures labeled as "Before" and "After." The left figure includes a shape positioned within a grid, and the right figure illustrates the transformed shape after reflecting across a dashed red line. This showcases how an object can be flipped over a line while maintaining its size and shape but changing its orientation. |
Definition of Transformations |
|
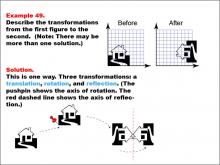
Math Example--Geometric Transformation--Transformations: Example 49 | Math Example--Geometric Transformation--Transformations: Example 49TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows two house-shaped figures on a grid. The "Before" figure is on the left, and the "After" figure is on the right. The transformation involves three steps: first, a translation moves the shape, then a rotation turns it around an axis marked by a pushpin, and finally, a reflection flips it across a dashed red line representing the axis of reflection. |
Definition of Transformations |
|
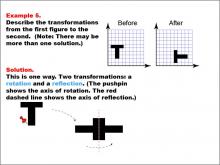
Math Example--Geometric Transformation--Transformations: Example 5 | Math Example--Geometric Transformation--Transformations: Example 5TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. Two grids labeled "Before" and "After" show a black "T" shape in different orientations. The shape first undergoes a rotation, indicated by a pushpin showing the axis of rotation, and then a reflection, shown by a red dashed line representing the axis of reflection. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
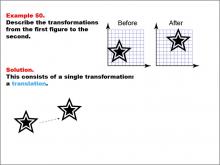
Math Example--Geometric Transformation--Transformations: Example 50 | Math Example--Geometric Transformation--Transformations: Example 50TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. The image shows two star-shaped figures on a grid. The "Before" figure is on the left, and the "After" figure is on the right. The transformation consists of a simple translation from left to right, showcasing how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
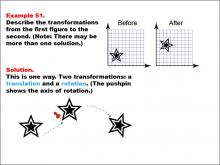
Math Example--Geometric Transformation--Transformations: Example 51 | Math Example--Geometric Transformation--Transformations: Example 51TopicTransformations DescriptionThis example illustrates a combination of translation and rotation in geometric transformations. The image shows two star-shaped figures on a grid. The "Before" figure is on the left, and the "After" figure is on the right. There are two transformations: first, a translation moves the shape, then a rotation turns it around an axis marked by a pushpin. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
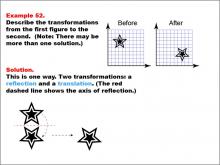
Math Example--Geometric Transformation--Transformations: Example 52 | Math Example--Geometric Transformation--Transformations: Example 52TopicTransformations DescriptionThis example demonstrates a combination of reflection and translation in geometric transformations. The image shows two star-shaped figures on a grid. The "Before" figure is on the left, and the "After" figure is on the right, located lower and to the right. There are two transformations: first, a reflection across an axis shown by a red dashed line, followed by a translation to move the shape to its final position. This illustrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
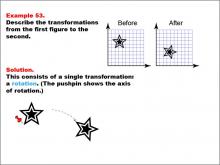
Math Example--Geometric Transformation--Transformations: Example 53 | Math Example--Geometric Transformation--Transformations: Example 53TopicTransformations DescriptionThis example demonstrates a single rotation in geometric transformations. The image shows a star on a grid labeled "Before" and "After." The star has been rotated to a new position on the grid, as indicated by a pushpin that marks the axis of rotation. This illustrates how an object can change its orientation without altering its size or shape. |
Definition of Transformations |
|
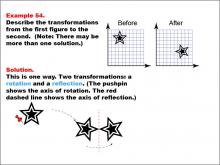
Math Example--Geometric Transformation--Transformations: Example 54 | Math Example--Geometric Transformation--Transformations: Example 54TopicTransformations DescriptionThis example illustrates a combination of rotation and reflection in geometric transformations. The image displays a star on a grid with "Before" and "After" labels. The transformation involves two steps: first, a rotation around an axis marked by a pushpin, and second, a reflection across a vertical axis shown by a red dashed line. This demonstrates how multiple transformations can be applied sequentially to create more complex changes in orientation and position. |
Definition of Transformations |
|
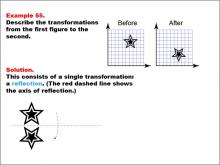
Math Example--Geometric Transformation--Transformations: Example 55 | Math Example--Geometric Transformation--Transformations: Example 55TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. In this image, a star is shown before and after undergoing a reflection. The red dashed line represents the axis of reflection, which is horizontal in this case. This showcases how an object can be flipped over a line while maintaining its size and shape but changing its orientation. |
Definition of Transformations |
|
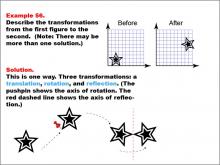
Math Example--Geometric Transformation--Transformations: Example 56 | Math Example--Geometric Transformation--Transformations: Example 56TopicTransformations DescriptionThis example demonstrates a complex combination of transformations: translation, rotation, and reflection. The image shows three transformations applied to the star: first, a translation moves the star to another position, then a rotation turns it around an axis indicated by a pushpin, and finally a reflection flips it across a vertical axis shown by a red dashed line. This illustrates how multiple transformations can be applied sequentially to create more complex changes in position and orientation. |
Definition of Transformations |
|
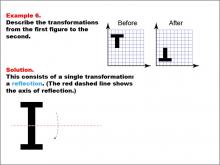
Math Example--Geometric Transformation--Transformations: Example 6 | Math Example--Geometric Transformation--Transformations: Example 6TopicTransformations DescriptionThis example demonstrates a single reflection in geometric transformations. Two grids labeled "Before" and "After" show a black "T" shape in different orientations. The solution diagram below illustrates a reflection of the shape across a red dashed line, which represents the axis of reflection. This transformation showcases how an object can be flipped over a line while maintaining its size and shape. |
Definition of Transformations |
|
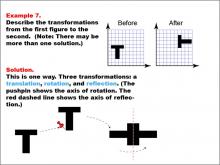
Math Example--Geometric Transformation--Transformations: Example 7 | Math Example--Geometric Transformation--Transformations: Example 7TopicTransformations DescriptionThis example illustrates a complex combination of transformations: translation, rotation, and reflection. Two grids labeled "Before" and "After" show a black "T" shape in different orientations. The solution diagram below demonstrates three sequential transformations: first, a translation moves the shape, then a rotation turns it (indicated by a pushpin showing the axis of rotation), and finally, a reflection flips it across a red dashed line representing the axis of reflection. |
Definition of Transformations |
|
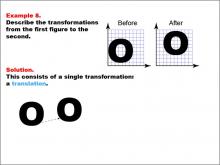
Math Example--Geometric Transformation--Transformations: Example 8 | Math Example--Geometric Transformation--Transformations: Example 8TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two grids labeled "Before" and "After" show an "O" shape slightly shifted between the grids. The solution diagram below illustrates a translation of the shape from one position to another, showcasing how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
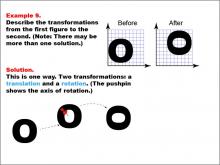
Math Example--Geometric Transformation--Transformations: Example 9 | Math Example--Geometric Transformation--Transformations: Example 9TopicTransformations DescriptionThis example illustrates a combination of transformations: translation and rotation. Two circular "O" shapes are shown on a grid, one labeled "Before" and the other "After". The solution involves a translation (movement) and a rotation, with a pushpin indicating the axis of rotation. This demonstrates how multiple transformations can be applied sequentially to a shape. |
Definition of Transformations |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 1 | Equations Using the Exterior Angle Theorem--Example 1TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 10 | Equations Using the Exterior Angle Theorem--Example 10TopicEquations DescriptionThis example illustrates a more complex application of the Exterior Angle Theorem in solving triangle-related equations. In this scenario, we have a triangle with one known interior angle of 35°, an unknown interior angle y, and an unknown exterior angle x. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Here, the equation is set up as x = 35° + y. Furthermore, the angles 3x and x are supplementary, allowing you to solve for x. Having solved for x, you can then solve for y. |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 2 | Equations Using the Exterior Angle Theorem--Example 2TopicEquations |
Applications of Triangles |
|
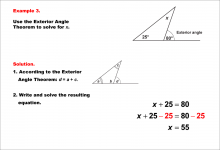
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 3 | Equations Using the Exterior Angle Theorem--Example 3TopicEquations |
Applications of Triangles |
|
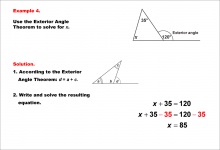
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 4 | Equations Using the Exterior Angle Theorem--Example 4TopicEquations |
Applications of Triangles |
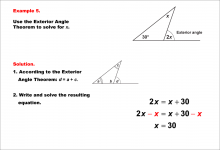
|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 5 | Equations Using the Exterior Angle Theorem--Example 5TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 6 | Equations Using the Exterior Angle Theorem--Example 6TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 7 | Equations Using the Exterior Angle Theorem--Example 7TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 8 | Equations Using the Exterior Angle Theorem--Example 8TopicEquations |
Applications of Triangles |

|
Math Example--Solving Equations--Equations Using the Exterior Angle Theorem--Example 9 | Equations Using the Exterior Angle Theorem--Example 9TopicEquations DescriptionThis example presents a more challenging application of the Exterior Angle Theorem in solving triangle-related equations. In this scenario, we have a triangle with one known interior angle of 25°, an unknown interior angle y, and an unknown exterior angle x. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Here, the equation is set up as x = 25° + y. You can also use the fact that x and 2x are supplementary, allowing you to solve for x. By solving for x, you can then solve for y using the triangle equation. |
Applications of Triangles |
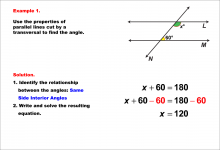
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 1 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 1TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
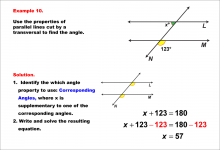
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 10 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 10TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
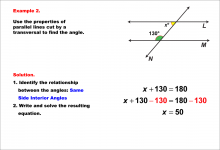
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 2 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 2TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
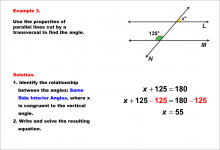
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 3 | TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
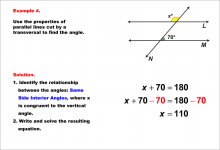
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 4 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 4TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
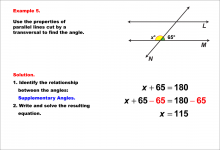
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 5 | TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
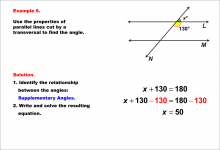
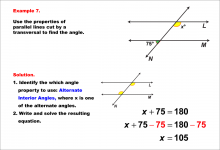
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 6 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 6TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
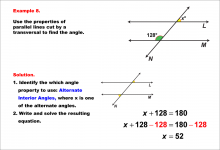
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 7 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 7TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
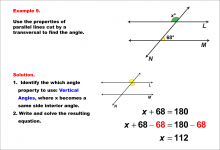
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 8 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 8TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
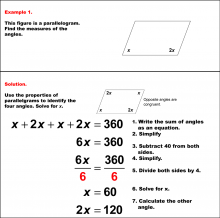
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 9 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 9TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 1 | Solving Equations with Angle Measures 2--Example 1TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 10 | Solving Equations with Angle Measures 2--Example 10TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
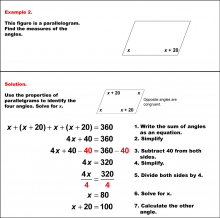
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 2 | Solving Equations with Angle Measures 2--Example 2TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
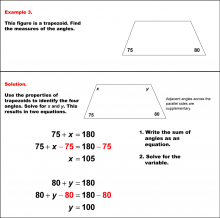
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 3 | Solving Equations with Angle Measures 2--Example 3TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
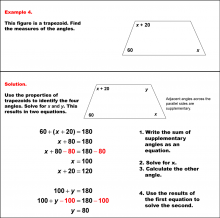
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4 | Solving Equations with Angle Measures 2--Example 4TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
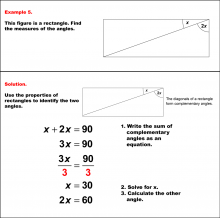
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 5 | Solving Equations with Angle Measures 2--Example 5TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 6 | Solving Equations with Angle Measures 2--Example 6TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
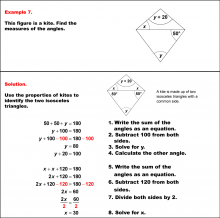
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 7 | Solving Equations with Angle Measures 2--Example 7TopicEquations DescriptionThis example demonstrates solving equations involving angle measures in a kite. A kite has two pairs of adjacent congruent angles. In this case, we have angles represented as (x+50)°, (x+50)°, (y+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the sum of the angles of a triangle is 180°. You can use the triangle equation to solve for y. Once you determine the value for y, you can use that to find x using either the triangle or the quadrilateral equation. In the solution shown, the triangle equation is used. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
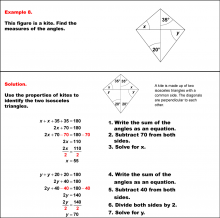
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 8 | Solving Equations with Angle Measures 2--Example 8TopicEquations DescriptionThis example illustrates solving equations involving angle measures in a kite. The kite has two known angles of 70° and 40°, and two unknown angles represented as (x+y)°. To solve this problem, we look at the triangles formed by one of the diagonals of the kite and use the triangle equation. First solve for x with the top triangle. Once you find x, use that value to solve for y in the bottom triangle. You could also use the quadrilateral equation to solve for y. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
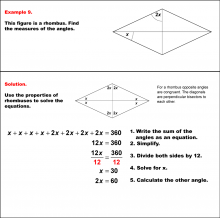
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 9 | Solving Equations with Angle Measures 2--Example 9TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |