
Illustrative Math Alignment: Grade 7 Unit 7
Expressions, Equations, and Inequalities
Lesson 9: Dealing with Negative Numbers
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
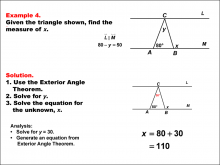
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4 | Solving Equations Using Triangle Properties: Example 4TopicEquations DescriptionThis example demonstrates solving equations using the Exterior Angle Theorem in the context of parallel lines cut by a transversal, two crucial concepts in geometry. The problem presents a triangle with two known interior angles of 80° and y, and an unknown exterior angle x°. We are also given that 80 - y = 50, which simplifies to y = 30. The goal is to determine the value of x using the properties of triangles and the Exterior Angle Theorem. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Wo we get x = 80 + 30, or x = 110. |
Applications of Equations and Inequalities and Applications of Triangles |
|
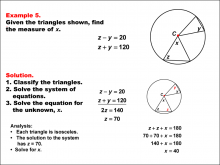
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 5 | Solving Equations Using Triangle Properties: Example 5TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles centered in a circle. The problem presents two equations: z - y = 20 and z + y = 120, where z and y represent angles in the isosceles triangles. The goal is to solve this system of equations to find the values of z and y, utilizing properties of isosceles triangles and circles. |
Applications of Equations and Inequalities and Applications of Triangles |
|
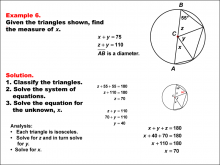
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 6 | Solving Equations Using Triangle Properties: Example 6TopicEquations DescriptionThis example explores solving equations involving triangles that share a vertex at the center of a circle. We are presented with two equations: x + y = 75 and z + y = 110, where x, y, and z represent angles in the triangle The goal is to solve this system of equations to find the values of x, y, and z, utilizing properties of isosceles triangles. Since each of the triangles is isosceles, we know that z + 55 + 55 = 180 and therefore, z = 70°. We substitute this into one of the equations: 70 + y = 110 7 = 40° |
Applications of Equations and Inequalities and Applications of Triangles |
|
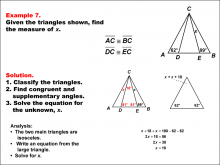
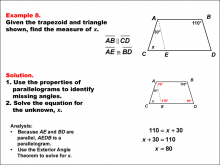
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 7 | Solving Equations Using Triangle Properties: Example 7TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles with a common vertex and base. We are given two angles, 62° and 99°, and need to find the unknown angle x. This problem demonstrates how to use the properties of isosceles triangles and the sum of angles in a triangle to solve for an unknown angle. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
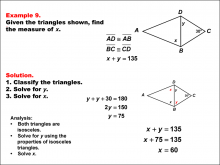
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 8 | Solving Equations Using Triangle Properties: Example 8TopicEquations DescriptionThis example involves solving an equation using the properties of a trapezoid with an embedded parallelogram and applying the exterior angle theorem. We are given two angles, 30° and 110°, and need to find the unknown angle x. This problem demonstrates the application of multiple geometric concepts to solve a complex equation. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
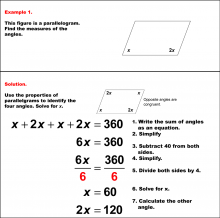
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 9 | Solving Equations Using Triangle Properties: Example 9TopicEquations DescriptionThis example focuses on solving equations using the properties of a kite and applying the exterior angle theorem. We are given one angle of 30° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 1 | Solving Equations with Angle Measures 2--Example 1TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
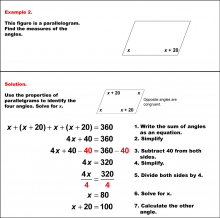
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 10 | Solving Equations with Angle Measures 2--Example 10TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 2 | Solving Equations with Angle Measures 2--Example 2TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
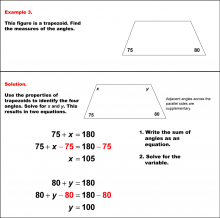
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 3 | Solving Equations with Angle Measures 2--Example 3TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
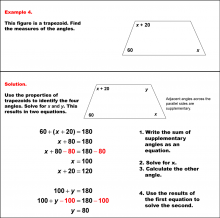
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4 | Solving Equations with Angle Measures 2--Example 4TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
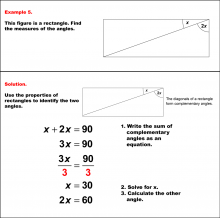
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 5 | Solving Equations with Angle Measures 2--Example 5TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 6 | Solving Equations with Angle Measures 2--Example 6TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
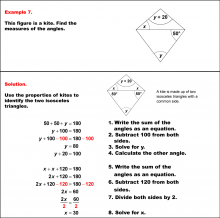
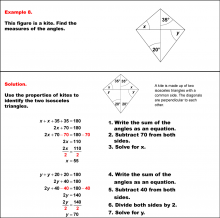
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 7 | Solving Equations with Angle Measures 2--Example 7TopicEquations DescriptionThis example demonstrates solving equations involving angle measures in a kite. A kite has two pairs of adjacent congruent angles. In this case, we have angles represented as (x+50)°, (x+50)°, (y+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the sum of the angles of a triangle is 180°. You can use the triangle equation to solve for y. Once you determine the value for y, you can use that to find x using either the triangle or the quadrilateral equation. In the solution shown, the triangle equation is used. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
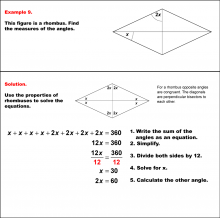
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 8 | Solving Equations with Angle Measures 2--Example 8TopicEquations DescriptionThis example illustrates solving equations involving angle measures in a kite. The kite has two known angles of 70° and 40°, and two unknown angles represented as (x+y)°. To solve this problem, we look at the triangles formed by one of the diagonals of the kite and use the triangle equation. First solve for x with the top triangle. Once you find x, use that value to solve for y in the bottom triangle. You could also use the quadrilateral equation to solve for y. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 9 | Solving Equations with Angle Measures 2--Example 9TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 11 | Solving Equations with Angle Measures--Example 11TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12 | Solving Equations with Angle Measures--Example 12TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 13 | Solving Equations with Angle Measures--Example 13TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 14 | Solving Equations with Angle Measures--Example 14TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
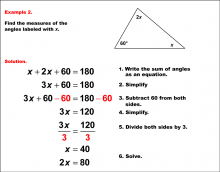
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 15 | Solving Equations with Angle Measures--Example 15TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 2 | Solving Equations with Angle Measures--Example 2TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3 | Solving Equations with Angle Measures--Example 3TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 4 | Solving Equations with Angle Measures--Example 4TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
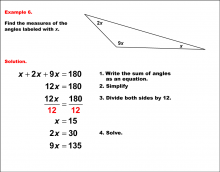
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 5 | Solving Equations with Angle Measures--Example 5TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 6 | Solving Equations with Angle Measures--Example 6TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 7 | Solving Equations with Angle Measures--Example 7TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 8 | Solving Equations with Angle Measures--Example 8TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9 | Solving Equations with Angle Measures--Example 9TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Radical Equations--Example 1 | Solving Radical Equations--Example 1TopicEquations DescriptionThis example demonstrates solving a basic radical equation involving a square root. Solving it involves squaring both sides of the equation. Sometimes this introduces an extraneous solution. In this case it doesn't. This is a legitimate solution. For a complete collection of math examples related to Solving Radical Equations click on this link: Math Examples: Solving Radical Equations Collection. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 2 | Solving Radical Equations--Example 2TopicEquations DescriptionThis example shows an equation with a square root with the x-term under the radical. Solving it involves squaring both sides. Sometimes this introduces an extraneous solution, but in this case the solution is real. For a complete collection of math examples related to Solving Radical Equations click on this link: Math Examples: Solving Radical Equations Collection. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 3 | Solving Radical Equations--Example 3TopicEquations DescriptionThis example demonstrates solving a radical equation with a real solution. Because both sides of the equation are squared, sometimes extraneous solutions are introduced, but in this case there is a real solution. For a complete collection of math examples related to Solving Radical Equations click on this link: Math Examples: Solving Radical Equations Collection. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 4 | Solving Radical Equations--Example 4TopicEquations DescriptionThis example showcases solving a radical equation involving a square root with an extraneous solution. Such solutions are introduced when both sides of the equation are solved. For a complete collection of math examples related to Solving Radical Equations click on this link: Math Examples: Solving Radical Equations Collection. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 5 | Solving Radical Equations--Example 5TopicEquations DescriptionThis example demonstrates solving a radical equation with an x-term inside the radical. Solving equations of this sort often involves squaring both sides. For a complete collection of math examples related to Solving Radical Equations click on this link: Math Examples: Solving Radical Equations Collection. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 6 | Solving Radical Equations--Example 6TopicEquations DescriptionThis example demonstrates a radical equation with an extraneous solution. Such solutions are often introduced when both sides of an equation are squared. For a complete collection of math examples related to Solving Radical Equations click on this link: Math Examples: Solving Radical Equations Collection. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 7 | Solving Radical Equations--Example 7TopicEquations DescriptionThis example demonstrates solving a radical equation with an x-term inside the radical and an x-term outside the radical. Solving equations of this sort often involves squaring both sides. However, it's crucial to check these solutions in the original equation, as the process of squaring can introduce extraneous solutions. This example demonstrates how solving radical equations can lead to higher-degree polynomial equations, requiring additional algebraic skills. |
Radical Functions and Equations |

|
Math Example--Solving Equations--Solving Radical Equations--Example 8 | Solving Radical Equations--Example 8TopicEquations DescriptionThis example demonstrates solving a radical equation with an x-term inside the radical and an x-term outside the radical. Solving equations of this sort often involves squaring both sides. However, it's crucial to check these solutions in the original equation, as the process of squaring can introduce extraneous solutions. This example demonstrates how solving radical equations can lead to higher-degree polynomial equations, requiring additional algebraic skills. |
Radical Functions and Equations |
|
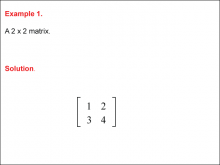
Math Example--Systems of Equations--Matrices--Example 1 | Math Example--Systems of Equations--Matrices--Example 1
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 2 | Math Example--Systems of Equations--Matrices--Example 2
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 3 | Math Example--Systems of Equations--Matrices--Example 3
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 4 | Math Example--Systems of Equations--Matrices--Example 4
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 5 | Math Example--Systems of Equations--Matrices--Example 5
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 6 | Math Example--Systems of Equations--Matrices--Example 6
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 7 | Math Example--Systems of Equations--Matrices--Example 7
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Matrices--Example 8 | Math Example--Systems of Equations--Matrices--Example 8
This is part of a collection of math examples that focus on systems of equations. |
Numerical and Algebraic Expressions |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 1 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 1TopicSystems of Equations DescriptionThis image demonstrates solving the system y = 20x + 1 and y = 4x + 1 using elimination. The equations are manipulated by multiplying the second equation by -5 to align coefficients, yielding -5y = -20x - 5. Adding the equations eliminates x, resulting in -4y = -4 or y = 1. Substituting y = 1 into y = 20x + 1 solves x = 0. The intersection point is (0, 1). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 10 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 10TopicSystems of Equations DescriptionThe system y = x + 4 and y = 2x - 5 is solved using elimination. Multiplying the first equation by -2 gives -2y = -2x - 8. Adding cancels x, resulting in -y = -13 or y = 13. Substituting y = 13 into y = x + 4 finds x = 9. The solution is (9, 13). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |

|
Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 2 | Math Example--Systems of Equations--Solving Linear Systems by Elimination: Example 2TopicSystems of Equations DescriptionThis example explains solving y = -12x + 7 and y = -6x + 1 through elimination. The second equation is multiplied by -2, giving -2y = 12x - 2. Adding eliminates x, producing -y = 5 or y = -5. Substituting y = -5 into y = -12x + 7 solves x = 1. The solution is (1, -5). Linear systems of equations are fundamental in algebra, providing a means to analyze and predict relationships between variables. By exploring worked-out examples, students gain confidence and clarity in solving these systems. |
Solving Systems of Equations |