
Illustrative Math Alignment: Grade 8 Unit 1
Rigid Transformations and Congruence
Lesson 16: Parallel Lines and the Angles in a Triangle
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
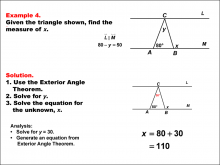
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4 | Solving Equations Using Triangle Properties: Example 4TopicEquations DescriptionThis example demonstrates solving equations using the Exterior Angle Theorem in the context of parallel lines cut by a transversal, two crucial concepts in geometry. The problem presents a triangle with two known interior angles of 80° and y, and an unknown exterior angle x°. We are also given that 80 - y = 50, which simplifies to y = 30. The goal is to determine the value of x using the properties of triangles and the Exterior Angle Theorem. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Wo we get x = 80 + 30, or x = 110. |
Applications of Equations and Inequalities and Applications of Triangles |
|
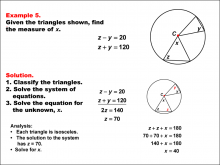
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 5 | Solving Equations Using Triangle Properties: Example 5TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles centered in a circle. The problem presents two equations: z - y = 20 and z + y = 120, where z and y represent angles in the isosceles triangles. The goal is to solve this system of equations to find the values of z and y, utilizing properties of isosceles triangles and circles. |
Applications of Equations and Inequalities and Applications of Triangles |
|
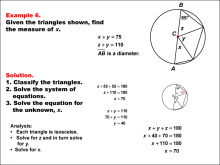
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 6 | Solving Equations Using Triangle Properties: Example 6TopicEquations DescriptionThis example explores solving equations involving triangles that share a vertex at the center of a circle. We are presented with two equations: x + y = 75 and z + y = 110, where x, y, and z represent angles in the triangle The goal is to solve this system of equations to find the values of x, y, and z, utilizing properties of isosceles triangles. Since each of the triangles is isosceles, we know that z + 55 + 55 = 180 and therefore, z = 70°. We substitute this into one of the equations: 70 + y = 110 7 = 40° |
Applications of Equations and Inequalities and Applications of Triangles |
|
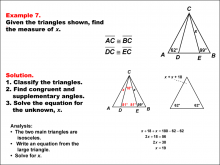
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 7 | Solving Equations Using Triangle Properties: Example 7TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles with a common vertex and base. We are given two angles, 62° and 99°, and need to find the unknown angle x. This problem demonstrates how to use the properties of isosceles triangles and the sum of angles in a triangle to solve for an unknown angle. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
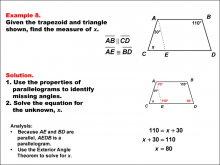
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 8 | Solving Equations Using Triangle Properties: Example 8TopicEquations DescriptionThis example involves solving an equation using the properties of a trapezoid with an embedded parallelogram and applying the exterior angle theorem. We are given two angles, 30° and 110°, and need to find the unknown angle x. This problem demonstrates the application of multiple geometric concepts to solve a complex equation. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
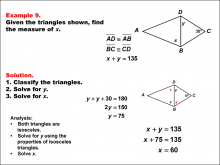
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 9 | Solving Equations Using Triangle Properties: Example 9TopicEquations DescriptionThis example focuses on solving equations using the properties of a kite and applying the exterior angle theorem. We are given one angle of 30° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
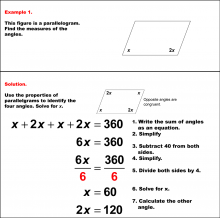
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 1 | Solving Equations with Angle Measures 2--Example 1TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
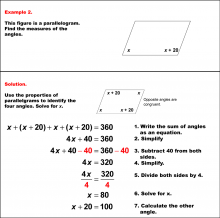
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 10 | Solving Equations with Angle Measures 2--Example 10TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 2 | Solving Equations with Angle Measures 2--Example 2TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
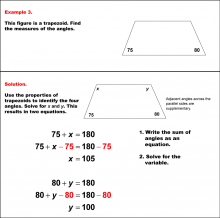
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 3 | Solving Equations with Angle Measures 2--Example 3TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
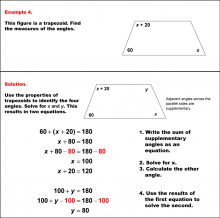
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4 | Solving Equations with Angle Measures 2--Example 4TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
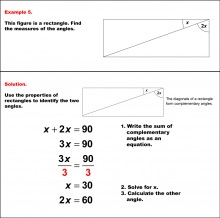
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 5 | Solving Equations with Angle Measures 2--Example 5TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 6 | Solving Equations with Angle Measures 2--Example 6TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
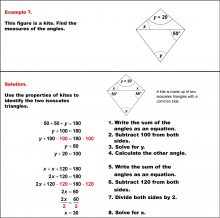
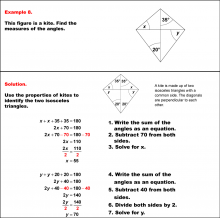
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 7 | Solving Equations with Angle Measures 2--Example 7TopicEquations DescriptionThis example demonstrates solving equations involving angle measures in a kite. A kite has two pairs of adjacent congruent angles. In this case, we have angles represented as (x+50)°, (x+50)°, (y+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the sum of the angles of a triangle is 180°. You can use the triangle equation to solve for y. Once you determine the value for y, you can use that to find x using either the triangle or the quadrilateral equation. In the solution shown, the triangle equation is used. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
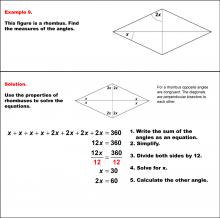
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 8 | Solving Equations with Angle Measures 2--Example 8TopicEquations DescriptionThis example illustrates solving equations involving angle measures in a kite. The kite has two known angles of 70° and 40°, and two unknown angles represented as (x+y)°. To solve this problem, we look at the triangles formed by one of the diagonals of the kite and use the triangle equation. First solve for x with the top triangle. Once you find x, use that value to solve for y in the bottom triangle. You could also use the quadrilateral equation to solve for y. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 9 | Solving Equations with Angle Measures 2--Example 9TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 11 | Solving Equations with Angle Measures--Example 11TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12 | Solving Equations with Angle Measures--Example 12TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 13 | Solving Equations with Angle Measures--Example 13TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 14 | Solving Equations with Angle Measures--Example 14TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
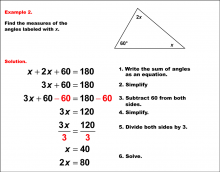
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 15 | Solving Equations with Angle Measures--Example 15TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 2 | Solving Equations with Angle Measures--Example 2TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3 | Solving Equations with Angle Measures--Example 3TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 4 | Solving Equations with Angle Measures--Example 4TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
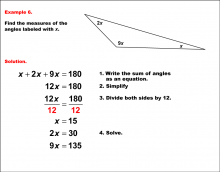
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 5 | Solving Equations with Angle Measures--Example 5TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 6 | Solving Equations with Angle Measures--Example 6TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 7 | Solving Equations with Angle Measures--Example 7TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 8 | Solving Equations with Angle Measures--Example 8TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9 | Solving Equations with Angle Measures--Example 9TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
MATH EXAMPLES--Teacher's Guide: Quadrilateral Classification | MATH EXAMPLES--Teacher's Guide: Quadrilateral Classification
This set of tutorials provides 34 examples of the types of quadrilaterals and how to classify quadrilaterals based on the sides and angles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Definition of a Quadrilateral |

|
MATH EXAMPLES--Teacher's Guide: Right Triangles | MATH EXAMPLES--Teacher's Guide: Right Triangles
This set of tutorials provides 26 examples of how to find the length of a side of a triangle using given angle or side measurements. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Right Triangles |

|
MATH EXAMPLES--Teacher's Guide: Triangle Area and Perimeter | MATH EXAMPLES--Teacher's Guide: Triangle Area and Perimeter
This set of tutorials provides 40 examples of how to find the area and perimeter of triangles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Area and Perimeter of Triangles |

|
MATH EXAMPLES--Teacher's Guide: Triangle Classification | MATH EXAMPLES--Teacher's Guide: Triangle Classification
This set of tutorials provides 24 examples that show how to identify different types of triangles and how to solve for x using the properties of triangles. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Definition of a Triangle |

|
MATH EXAMPLES--Triangle Area and Perimeter | MATH EXAMPLES--Triangle Area and Perimeter
This set of tutorials provides 40 examples of how to find the area and perimeter of triangles. NOTE: The download is a PPT file. |
Area and Perimeter of Triangles |

|
MATH EXAMPLES--Triangle Classification | MATH EXAMPLES--Triangle Classification
This set of tutorials provides 24 examples that show how to identify different types of triangles and how to solve for x using the properties of triangles. NOTE: The download is a PPT file. |
Definition of a Triangle |

|
Test Prep Interactive Quiz--Classifying Angles | Test Prep Interactive Quiz--Classifying Angles
This is part of a collection of self-scoring interactive math quizzes on a variety of topics. To see the complete of these quizzes, click on this link. Note: The download is the teacher's guide.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Definition of an Angle |

|
Video Transcript: Desmos Geometry Exploration: Triangle Basics | Video Transcript: Desmos Geometry Exploration: Triangle Basics
This is the transcript for the video entitled, Desmos Geometry Exploration: Triangle Basics. In this video tutorial the basics of triangles are explored. Students are then shown how to construct triangles using the Desmos geometry tools. This is part of a collection of video transcript for the video tutorial series on using the Desmos Geometry Tools. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
Video Transcript: Geometry Applications: Triangles | Video Transcript: Geometry Applications: Triangles
This is the transcript for the video of same title. Video contents: In this program we explore the properties of triangle. We do this in the context of two real-world applications. In the first, we explore the triangular trusses in the Eiffel Tower and in the process learn about key properties of triangles. In the second application, we look at right-triangle-shaped sails on sail boat and why these are the ideal shape for efficient sailing. |
Applications of Triangles |

|
Video Transcript: Geometry Applications: Triangles, Segment 1: Introduction | Video Transcript: Geometry Applications: Triangles, Segment 1: Introduction
This is the transcript for the video of same title. Video contents: The Bank of China building in Hong Kong is a dramatic example of triangular support. The notion of triangular trusses is introduced, along with the key concepts developed in the rest of the program. This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Applications of Triangles |

|
Video Transcript: Geometry Applications: Triangles, Segment 2: Triangles | Video Transcript: Geometry Applications: Triangles, Segment 2: Triangles
This is the transcript for the video of same title. Video contents: The Eiffel Tower includes quite a number of exposed triangular trusses. The properties of triangles are used to explore and explain the frequent use of triangular trusses in many building. In particular, isosceles and equilateral triangular trusses are explored. In addition triangle postulates and similarity are explored and analyzed. |
Applications of Triangles |

|
Video Transcript: TI-Nspire Mini-Tutorial: Circumscribing a Circle about a Triangle | Video Transcript: TI-Nspire Mini-Tutorial: Circumscribing a Circle about a Triangle
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Circumscribing a Circle about a Triangle. This is part of a collection of video transcripts for the video tutorial series on using the TI-Nspire Graphing Calculator. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Geometric Constructions with Triangles |

|
Video Transcript: TI-Nspire Mini-Tutorial: Constructing the Circumcenter of a Triangle | Video Transcript: TI-Nspire Mini-Tutorial: Constructing the Circumcenter of a Triangle
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Constructing the Circumcenter of a Triangle. This is part of a collection of video transcripts for the video tutorial series on using the TI-Nspire Graphing Calculator. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Geometric Constructions with Triangles |

|
Video Transcript: TI-Nspire Mini-Tutorial: Constructing the Orthocenter of a Triangle | Video Transcript: TI-Nspire Mini-Tutorial: Constructing the Orthocenter of a Triangle
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Constructing the Orthocenter of a Triangle. This is part of a collection of video transcripts for the video tutorial series on using the TI-Nspire Graphing Calculator. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Geometric Constructions with Triangles |

|
Video Tutorial: Desmos Geometry Exploration: Classifying Triangles by Angle | Video Tutorial: Desmos Geometry Exploration: Classifying Triangles by Angle
TopicGeometry DescriptionThe video classifies triangles by their angles, highlighting acute, right, and obtuse triangles. Using Desmos, viewers construct and manipulate triangles to understand these categories. Key terms include equiangular, isosceles, and base angles. Applications involve creating different types of triangles and analyzing their angle properties. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
Video Tutorial: Desmos Geometry Exploration: Triangle Basics | Video Tutorial: Desmos Geometry Exploration: Triangle Basics
TopicGeometry DescriptionTriangles are defined as three-sided closed figures with internal angles summing to 180°. The video demonstrates creating triangles with Desmos tools and exploring their properties. Key terms include vertices, line segments, and angles. Applications include constructing and measuring triangles to verify their angle sums. |
Definition of a Triangle and Geometric Constructions with Triangles |

|
Video Tutorial: Parallel Lines Cut by a Transversal: Example 1 | This is part of a collection of video tutorials on parallel lines cut by a transversal. Using the properties of these lines, the value of an unknown angle is calculated. Note: The download is a PDF template for use in modeling the examples shown in the videos. |
Parallel Lines |

|
Video Tutorial: Parallel Lines Cut by a Transversal: Example 2 | This is part of a collection of video tutorials on parallel lines cut by a transversal. Using the properties of these lines, the value of an unknown angle is calculated. Note: The download is a PDF template for use in modeling the examples shown in the videos. |
Parallel Lines |

|
Video Tutorial: Parallel Lines Cut by a Transversal: Example 3 | This is part of a collection of video tutorials on parallel lines cut by a transversal. Using the properties of these lines, the value of an unknown angle is calculated. Note: The download is a PDF template for use in modeling the examples shown in the videos. |
Parallel Lines |