Illustrative Math Alignment: Grade 6 Unit 7

Rational Numbers

Lesson 11: Points on the Coordinate Plane

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
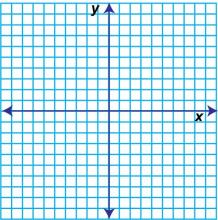
Math Clip Art--Geometry Concepts--Geometry Tools--Coordinate Grid	Math Clip Art--Geometry Tools--Coordinate Grid Topic Geometry Concepts Description This image features a coordinate grid, an essential tool in geometry for plotting points, lines, and shapes. The grid consists of horizontal and vertical lines that intersect at right angles, creating a series of squares. Coordinate grids are fundamental for understanding the Cartesian coordinate system, where each point is defined by an ordered pair (x, y). This system is widely used in mathematics, physics, engineering, and computer graphics to represent spatial relationships.	Exploring Coordinate Systems and Coordinate Systems
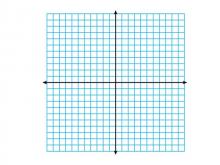
Math Clip Art--Geometry Concepts--Geometry Tools--Coordinate Grid--Blank	Math Clip Art--Geometry Tools--Coordinate Grid--Blank Topic Geometry Concepts Description This image shows a blank coordinate grid, serving as a versatile tool for plotting points, lines, and shapes in coordinate geometry. The grid provides a structured framework for visualizing mathematical concepts and relationships. Blank coordinate grids are commonly used in educational settings to teach students about graphing, transformations, and spatial reasoning. They allow for hands-on exploration of mathematical ideas and are essential for developing a deep understanding of the Cartesian coordinate system.	Exploring Coordinate Systems and Coordinate Systems
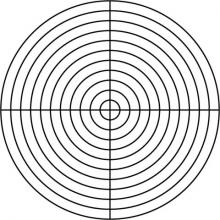
Math Clip Art--Geometry Concepts--Geometry Tools--Polar Coordinate Grid	Math Clip Art--Geometry Tools--Polar Coordinate Grid Topic Geometry Concepts Description This image features a polar coordinate grid, a tool used to represent points in a plane using a radius and an angle. Polar coordinates offer an alternative to Cartesian coordinates, particularly useful for circular and rotational problems. Polar coordinate grids are used in fields like physics, engineering, and navigation to solve problems involving circular motion and angular relationships. They provide a unique perspective on spatial relationships and are essential for understanding complex mathematical concepts.	Applications of Coordinate Geometry, Coordinate Systems and Applications of Points and Lines
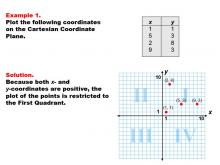
Math Example--Coordinate Geometry--Coordinate Systems: Example 1	Math Example--Coordinate Geometry--Coordinate Systems: Example 1 Topic Geometry Description In this example, we explore plotting coordinates on the Cartesian Coordinate Plane. The example demonstrates a Cartesian coordinate plane with four plotted points: (1, 1), (5, 3), (2, 8), and (9, 3). All points are in the first quadrant where both x and y are positive. Understanding coordinate geometry is crucial for developing a strong mathematical foundation. This collection offers several worked-out examples that clarify various aspects of plotting points on different coordinate systems.	Coordinate Systems
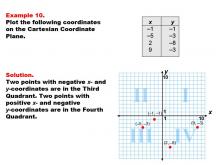
Math Example--Coordinate Geometry--Coordinate Systems: Example 10	Math Example--Coordinate Geometry--Coordinate Systems: Example 10 Topic Geometry Description This example illustrates plotting coordinates in both the third and fourth quadrants of the Cartesian Coordinate Plane. The image displays four points: (-1, -1) and (-5, -3) in the third quadrant, and (2, -8) and (9, -3) in the fourth quadrant. This example demonstrates how points can be distributed across quadrants that share a negative y-axis.	Coordinate Systems
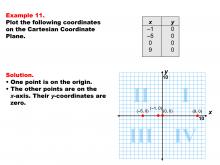
Math Example--Coordinate Geometry--Coordinate Systems: Example 11	Math Example--Coordinate Geometry--Coordinate Systems: Example 11 Topic Geometry Description This example focuses on plotting coordinates along the x-axis of the Cartesian Coordinate Plane. The image shows four points: (-1, 0), (-5, 0), (0, 0), and (9, 0). These points are all located on the x-axis, where the y-coordinate is always zero. Understanding how to plot points on the axes is a fundamental skill in coordinate geometry. This example helps students visualize the concept that all points on the x-axis have a y-coordinate of zero, regardless of their x-coordinate value.	Coordinate Systems
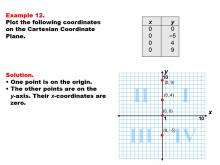
Math Example--Coordinate Geometry--Coordinate Systems: Example 12	Math Example--Coordinate Geometry--Coordinate Systems: Example 12 Topic Geometry Description This example demonstrates plotting coordinates along the y-axis of the Cartesian Coordinate Plane. The image displays four points: (0, 0), (0, -5), (0, 4), and (0, 9). These points are all situated on the y-axis, where the x-coordinate is always zero. Understanding how to plot points on the axes is a crucial skill in coordinate geometry. This example helps students visualize the concept that all points on the y-axis have an x-coordinate of zero, regardless of their y-coordinate value.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 13	Math Example--Coordinate Geometry--Coordinate Systems: Example 13 Topic Geometry Description This example illustrates plotting coordinates on both the x-axis and y-axis of the Cartesian Coordinate Plane. The image shows four points: (0, 0), (0, 4), (-6, 0), and (6, 0). These points are located on both axes, including the origin. Understanding how to plot points on both axes is essential in coordinate geometry. This example helps students visualize the concept that points on the x-axis have a y-coordinate of zero, while points on the y-axis have an x-coordinate of zero.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 14	Math Example--Coordinate Geometry--Coordinate Systems: Example 14 Topic Geometry Description This example introduces plotting coordinates on a polar coordinate grid. The image shows four points plotted with their polar coordinates (r, θ): (2, 45°), (3, 60°), (5, 75°), and (4, 15°). Each point is labeled with its respective coordinates on the grid. Understanding polar coordinates is crucial for many applications in mathematics and physics. This example helps students visualize how points are plotted using distance from the origin (r) and an angle (θ) instead of x and y coordinates.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 15	Math Example--Coordinate Geometry--Coordinate Systems: Example 15 Topic Geometry Description This example demonstrates plotting coordinates on a polar coordinate grid with angles between 90° and 180°. The image displays four points with their polar coordinates (r, θ): (2, 105°), (3, 120°), (5, 165°), and (4, 135°). The grid shows angles from 0° to 360°. Understanding how to plot points in different quadrants of a polar grid is essential for mastering polar coordinates. This example helps students visualize how points are positioned when their angles are between 90° and 180°, corresponding to the second quadrant in a Cartesian system.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 16	Math Example--Coordinate Geometry--Coordinate Systems: Example 16 Topic Geometry Description This example focuses on plotting coordinates on a polar coordinate grid with angles between 180° and 270°. The image shows four points with their polar coordinates (r, θ): (2, 195°), (3, 210°), (5, 255°), and (4, 225°). The grid highlights angles in this specific range. Understanding how to plot points in different quadrants of a polar grid is crucial for mastering polar coordinates. This example helps students visualize how points are positioned when their angles are between 180° and 270°, corresponding to the third quadrant in a Cartesian system.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 17	Math Example--Coordinate Geometry--Coordinate Systems: Example 17 Topic Geometry Description This example illustrates plotting coordinates on a polar coordinate grid with angles between 270° and 360°. The image displays four points with their polar coordinates (r, θ): (2, 285°), (3, 300°), (5, 345°), and (4, 315°). The grid focuses on plotting angles in this specific range. Understanding how to plot points in different quadrants of a polar grid is essential for mastering polar coordinates. This example helps students visualize how points are positioned when their angles are between 270° and 360°, corresponding to the fourth quadrant in a Cartesian system.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 18	Math Example--Coordinate Geometry--Coordinate Systems: Example 18 Topic Geometry Description This example demonstrates plotting coordinates on a polar coordinate grid using negative angles. The image shows four points with their polar coordinates (r, θ): (2, -75°), (3, -60°), (5, -15°), and (4, -45°). The grid displays angles in both positive and negative directions, illustrating how negative angles are equivalent to positive ones. Understanding negative angles in polar coordinates is crucial for a comprehensive grasp of this system. This example helps students visualize how negative angles are measured clockwise, contrary to the standard counterclockwise measurement of positive angles.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 19	Math Example--Coordinate Geometry--Coordinate Systems: Example 19 Topic Geometry Description This example focuses on plotting coordinates on a polar coordinate grid using negative angles in the second quadrant. The image displays four points with their polar coordinates (r, θ): (2, -165°), (3, -150°), (5, -105°), and (4, -135°). These negative angles correspond to points in the second quadrant of a Cartesian plane. Understanding how to plot points using negative angles in different quadrants is essential for mastering polar coordinates. This example helps students visualize how negative angles in this range relate to positive angles and their position on the grid.	Coordinate Systems
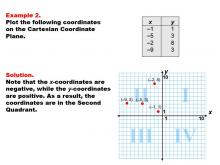
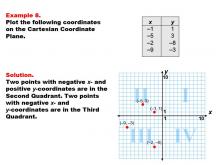
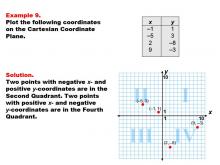
Math Example--Coordinate Geometry--Coordinate Systems: Example 2	Math Example--Coordinate Geometry--Coordinate Systems: Example 2 Topic Geometry Description This example focuses on plotting coordinates in the second quadrant of the Cartesian Coordinate Plane. The image shows four points: (-1, 1), (-5, 3), (-2, 8), and (-9, 3). All these points have negative x-coordinates and positive y-coordinates, placing them in the second quadrant. Understanding how to plot points in different quadrants is crucial for mastering coordinate geometry. This collection of examples helps students visualize the relationship between coordinate pairs and their positions on the plane, particularly in the second quadrant where x is negative and y is positive.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 20	Math Example--Coordinate Geometry--Coordinate Systems: Example 20 Topic Geometry Description This example illustrates plotting coordinates on a polar coordinate grid using negative angles in the third quadrant. The image shows four points with their polar coordinates (r, θ): (2, -255°), (3, -240°), (5, -195°), and (4, -225°). These negative angles correspond to points in the third quadrant of a Cartesian plane. Understanding how to plot points using negative angles in different quadrants is crucial for a comprehensive grasp of polar coordinates. This example helps students visualize how negative angles in this range relate to positive angles and their position on the grid.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 21	Math Example--Coordinate Geometry--Coordinate Systems: Example 21 Topic Geometry Description This example demonstrates plotting coordinates on a polar coordinate grid using negative angles in the fourth quadrant. The image displays four points with their polar coordinates (r, θ): (2, -315°), (3, -300°), (5, -285°), and (4, -345°). These negative angles correspond to points in the first quadrant of a Cartesian plane. Understanding how to plot points using negative angles in different quadrants is essential for mastering polar coordinates. This example helps students visualize how negative angles in this range relate to positive angles and their position on the grid.	Coordinate Systems
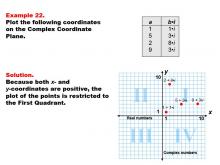
Math Example--Coordinate Geometry--Coordinate Systems: Example 22	Math Example--Coordinate Geometry--Coordinate Systems: Example 22 Topic Geometry Description This example introduces the concept of complex numbers on a coordinate plane. The image illustrates a complex coordinate plane with four points plotted in the first quadrant: 1 + 1i, 5 + 3i, 2 + 8i, and 9 + 3i. These points represent complex numbers with positive real and imaginary parts. Understanding complex numbers and their representation on a coordinate plane is crucial in advanced mathematics and various scientific fields. This example helps students visualize how complex numbers are plotted, with the real part on the x-axis and the imaginary part on the y-axis.	Coordinate Systems
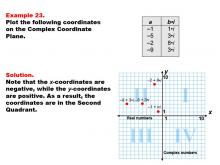
Math Example--Coordinate Geometry--Coordinate Systems: Example 23	Math Example--Coordinate Geometry--Coordinate Systems: Example 23 Topic Geometry Description This example focuses on plotting complex numbers in the second quadrant of the complex plane. The image shows four points: -1 + 1i, -5 + 3i, -2 + 8i, and -9 + 3i. These points represent complex numbers with negative real parts and positive imaginary parts. Understanding how to plot complex numbers in different quadrants is essential for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with negative real parts and positive imaginary parts are positioned on the complex plane.	Coordinate Systems
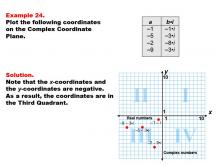
Math Example--Coordinate Geometry--Coordinate Systems: Example 24	Math Example--Coordinate Geometry--Coordinate Systems: Example 24 Topic Geometry Description This example demonstrates plotting complex numbers in the third quadrant of the complex plane. The image displays four points: -1 - 1i, -5 - 3i, -2 - 8i, and -9 - 3i. These points represent complex numbers with both negative real and imaginary parts. Understanding how to plot complex numbers in all quadrants is crucial for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with negative real and imaginary parts are positioned on the complex plane.	Coordinate Systems
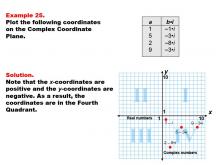
Math Example--Coordinate Geometry--Coordinate Systems: Example 25	Math Example--Coordinate Geometry--Coordinate Systems: Example 25 Topic Geometry Description This example illustrates plotting complex numbers in the fourth quadrant of the complex plane. The image shows four points: 1 - i, 5 - 3i, 2 - 8i, and 9 - 3i. These points represent complex numbers with positive real parts and negative imaginary parts. Understanding how to plot complex numbers in all quadrants is essential for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with positive real parts and negative imaginary parts are positioned on the complex plane.	Coordinate Systems
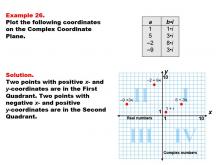
Math Example--Coordinate Geometry--Coordinate Systems: Example 26	Math Example--Coordinate Geometry--Coordinate Systems: Example 26 Topic Geometry Description This example demonstrates plotting complex numbers in both the first and second quadrants of the complex plane. The image shows four points: (1, i), (5, 3i), (-2, 8i), and (-9, 3i). These points represent complex numbers with varying real and imaginary parts. Understanding how to plot complex numbers across different quadrants is crucial for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with different combinations of positive and negative real and imaginary parts are positioned on the complex plane.	Coordinate Systems
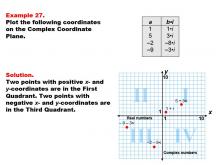
Math Example--Coordinate Geometry--Coordinate Systems: Example 27	Math Example--Coordinate Geometry--Coordinate Systems: Example 27 Topic Geometry Description This example illustrates plotting complex numbers in the first and third quadrants of the complex plane. The image displays four points: (1, i), (5, 3i), (-2, -8i), and (-9, -3i). These points represent complex numbers with varying real and imaginary parts. Understanding how to plot complex numbers across different quadrants is essential for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with different combinations of positive and negative real and imaginary parts are positioned on the complex plane.	Coordinate Systems
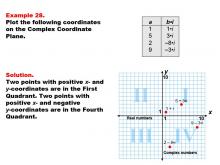
Math Example--Coordinate Geometry--Coordinate Systems: Example 28	Math Example--Coordinate Geometry--Coordinate Systems: Example 28 Topic Geometry Description This example focuses on plotting complex numbers in the first and fourth quadrants of the complex plane. The image shows four points: (1, i), (5, 3i), (2, -8i), and (9, -3i). These points represent complex numbers with positive real parts and varying imaginary parts. Understanding how to plot complex numbers across different quadrants is crucial for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with positive real parts and both positive and negative imaginary parts are positioned on the complex plane.	Coordinate Systems
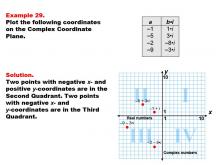
Math Example--Coordinate Geometry--Coordinate Systems: Example 29	Math Example--Coordinate Geometry--Coordinate Systems: Example 29 Topic Geometry Description This example demonstrates plotting complex numbers in the second and third quadrants of the complex plane. The image displays four points: (-1, i), (-5, 3i), (-2, -8i), and (-9, -3i). These points represent complex numbers with negative real parts and varying imaginary parts. Understanding how to plot complex numbers across different quadrants is essential for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with negative real parts and both positive and negative imaginary parts are positioned on the complex plane.	Coordinate Systems
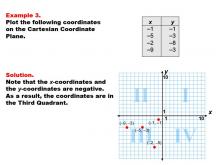
Math Example--Coordinate Geometry--Coordinate Systems: Example 3	Math Example--Coordinate Geometry--Coordinate Systems: Example 3 Topic Geometry Description This example demonstrates plotting coordinates in the third quadrant of the Cartesian Coordinate Plane. The image displays four points: (-1, -1), (-5, -3), (-2, -8), and (-9, -3). All these points have both negative x-coordinates and negative y-coordinates, situating them in the third quadrant. Coordinate geometry is a fundamental concept in mathematics, and understanding how to plot points in all quadrants is essential. This collection of examples helps students visualize the relationship between coordinate pairs and their positions on the plane, particularly in the third quadrant where both x and y are negative.	Coordinate Systems
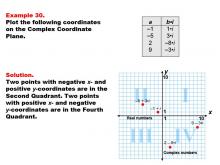
Math Example--Coordinate Geometry--Coordinate Systems: Example 30	Math Example--Coordinate Geometry--Coordinate Systems: Example 30 Topic Geometry Description This example illustrates plotting complex numbers in the second and fourth quadrants of the complex plane. The image shows four points: (-1, i), (-5, 3i), (2, -8i), and (9, -3i). These points represent complex numbers with varying real and imaginary parts. Understanding how to plot complex numbers across different quadrants is crucial for a comprehensive grasp of complex number theory. This example helps students visualize how complex numbers with different combinations of positive and negative real and imaginary parts are positioned on the complex plane.	Coordinate Systems
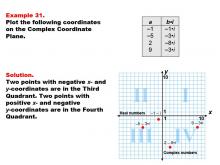
Math Example--Coordinate Geometry--Coordinate Systems: Example 31	Math Example--Coordinate Geometry--Coordinate Systems: Example 31 Topic Geometry Description This example focuses on plotting points in the third and fourth quadrants of the complex plane. The image displays four points: (-1, -i), (-5, -3i) in the third quadrant, and (2, -8i), (9, -3i) in the fourth quadrant. These points represent complex numbers with negative imaginary parts and varying real parts.	Coordinate Systems
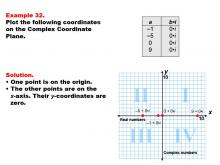
Math Example--Coordinate Geometry--Coordinate Systems: Example 32	Math Example--Coordinate Geometry--Coordinate Systems: Example 32 Topic Geometry Description This example demonstrates plotting points on the real axis of the complex plane. The image shows four points: (-5, 0), (-1, 0), (0, 0), and (9, 0). These points represent real numbers on the complex plane, where the imaginary part is zero. Understanding how to plot real numbers on the complex plane is crucial for developing a comprehensive grasp of complex number theory. This example helps students visualize that real numbers are a subset of complex numbers, lying on the real axis of the complex plane.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 33	Math Example--Coordinate Geometry--Coordinate Systems: Example 33 Topic Geometry Description This example illustrates plotting points on the imaginary axis of the complex plane. The image displays four points: (0, 0), (0, -5i), (0, 4i), and (0, 9i). These points represent purely imaginary numbers on the complex plane, where the real part is zero. Understanding how to plot purely imaginary numbers on the complex plane is essential for developing a comprehensive grasp of complex number theory. This example helps students visualize that purely imaginary numbers lie on the imaginary axis of the complex plane.	Coordinate Systems
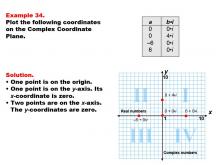
Math Example--Coordinate Geometry--Coordinate Systems: Example 34	Math Example--Coordinate Geometry--Coordinate Systems: Example 34 Topic Geometry Description This example demonstrates plotting points on both the real and imaginary axes of the complex plane. The image displays four points: (0, 0) at the origin, (0, 4i) on the imaginary axis, and (-6, 0) and (6, 0) on the real axis. These points represent a mix of real, imaginary, and the complex origin on the complex plane. Understanding how to plot points on both axes of the complex plane is crucial for developing a comprehensive grasp of complex number theory. This example helps students visualize the relationship between real and imaginary numbers within the complex plane, as well as the significance of the origin.	Coordinate Systems
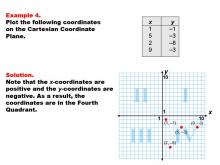
Math Example--Coordinate Geometry--Coordinate Systems: Example 4	Math Example--Coordinate Geometry--Coordinate Systems: Example 4 Topic Geometry Description This example illustrates plotting coordinates in the fourth quadrant of the Cartesian Coordinate Plane. The image shows four points: (1, -1), (5, -3), (2, -8), and (9, -3). All these points have positive x-coordinates and negative y-coordinates, placing them in the fourth quadrant. Understanding how to plot points in all quadrants of the Cartesian plane is essential for many areas of mathematics and science. This collection of examples helps students visualize the relationship between coordinate pairs and their positions on the plane, particularly in the fourth quadrant where x is positive and y is negative.	Coordinate Systems
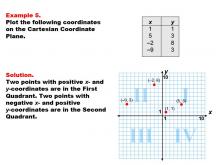
Math Example--Coordinate Geometry--Coordinate Systems: Example 5	Math Example--Coordinate Geometry--Coordinate Systems: Example 5 Topic Geometry Description This example showcases plotting coordinates in both the first and second quadrants of the Cartesian Coordinate Plane. The image displays four points: (1, 1) and (5, 3) in the first quadrant, and (-2, 8) and (-9, 3) in the second quadrant. This example demonstrates how points can be distributed across different quadrants based on their coordinates.	Coordinate Systems
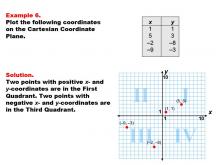
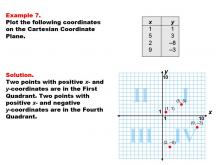
Math Example--Coordinate Geometry--Coordinate Systems: Example 6	Math Example--Coordinate Geometry--Coordinate Systems: Example 6 Topic Geometry Description This example illustrates plotting coordinates in both the first and third quadrants of the Cartesian Coordinate Plane. The image shows four points: (1, 1) and (5, 3) in the first quadrant, and (-2, -8) and (-9, -3) in the third quadrant. This example demonstrates how points can be distributed across opposite quadrants based on their coordinates.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 7	Math Example--Coordinate Geometry--Coordinate Systems: Example 7 Topic Geometry Description This example demonstrates plotting coordinates in both the first and fourth quadrants of the Cartesian Coordinate Plane. The image displays four points: (1, 1) and (5, 3) in the first quadrant, and (2, -8) and (9, -3) in the fourth quadrant. This example showcases how points can be distributed across quadrants that share a positive x-axis.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 8	Math Example--Coordinate Geometry--Coordinate Systems: Example 8 Topic Geometry Description This example illustrates plotting coordinates in both the second and third quadrants of the Cartesian Coordinate Plane. The image shows four points: (-1, 1) and (-5, 3) in the second quadrant, and (-2, -8) and (-9, -3) in the third quadrant. This example demonstrates how points can be distributed across quadrants that share a negative x-axis.	Coordinate Systems
Math Example--Coordinate Geometry--Coordinate Systems: Example 9	Math Example--Coordinate Geometry--Coordinate Systems: Example 9 Topic Geometry Description This example showcases plotting coordinates in both the second and fourth quadrants of the Cartesian Coordinate Plane. The image displays four points: (-1, 1) and (-5, 3) in the second quadrant, and (2, -8) and (9, -3) in the fourth quadrant. This example demonstrates how points can be distributed across quadrants that are diagonally opposite to each other.	Coordinate Systems
MATH EXAMPLES--Teacher's Guide: Coordinate Systems	MATH EXAMPLES--Teacher's Guide: Coordinate Systems This Teacher's Guide provides an overview of the 34 worked-out examples that show how to graph coordinates on Cartesian, Polar, and Complex coordinate planes. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Exploring Coordinate Systems and Coordinate Systems
Math in the News: Issue 98--Flight MH370	Math in the News: Issue 98--The Search for Missing Flight MH370 April 2014. In this issue of Math in the News we join the investigation in the missing flight MH370. We discuss the details of the flight and what we know so far. Using coordinate geometry, students can explore how experts narrow down the search area. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Exploring Coordinate Systems and Coordinate Systems
Math in the News: Issue 98--Flight MH370	Math in the News: Issue 98--The Search for Missing Flight MH370 April 2014. In this issue of Math in the News we join the investigation in the missing flight MH370. We discuss the details of the flight and what we know so far. Using coordinate geometry, students can explore how experts narrow down the search area. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Exploring Coordinate Systems and Coordinate Systems

Illustrative Math Alignment: Grade 6 Unit 7

Rational Numbers

Lesson 11: Points on the Coordinate Plane

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Related Resources

Related Resources

Related Resources