
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 3: Staying in Balance
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 10 | Solving Equations Using Angle Properties: Example 10TopicEquations DescriptionThis example illustrates solving equations using angle properties, focusing on parallel lines cut by a transversal and supplementary angles. When parallel lines are cut by a transversal, pairs of supplementary angles are formed, meaning they sum to 180°. In this scenario, we have one known angle of 118° and an unknown angle x. However, angle y and the 118° angle are alternate exterior angles, which are congruent. This means we can set up this equation using the property of supplementary angles: 118 + x = 180 |
Applications of Equations and Inequalities and Definition of an Angle |
|
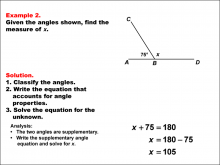
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 2 | Solving Equations Using Angle Properties: Example 2TopicEquations DescriptionThis example illustrates solving equations using angle properties, focusing on supplementary angles. Supplementary angles are two angles that sum to 180 degrees. In this scenario, we have one known angle of 75° and an unknown angle x. The equation for supplementary angles is always in the form: angle1 + angle2 = 180°. Here, we can write 75 + x = 180. To solve for x, we subtract 75 from both sides: x = 180 - 75, giving us x = 105°. |
Applications of Equations and Inequalities and Definition of an Angle |
|
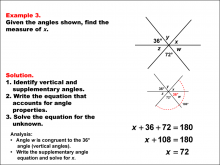
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 3 | Solving Equations Using Angle Properties: Example 3TopicEquations DescriptionThis example demonstrates solving equations using angle properties, specifically focusing on straight angles and vertical angles. A straight angle measures 180°, and vertical angles are always congruent. In this scenario, we have two known angles (36° and 72°) and an unknown angle x. This unknown angle x is vertical (and therefore congruent) to angle z. The angles 36, 72, and z form a straight, but since z is congruent to x, we can write the sum of this straight angle: x + 36 + 72 = 180 x = 72° |
Applications of Equations and Inequalities and Definition of an Angle |
|
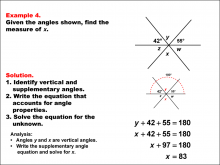
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 4 | Solving Equations Using Angle Properties: Example 4TopicEquations DescriptionThis example illustrates solving equations using angle properties, focusing on straight angles and vertical angles. A straight angle measures 180°, and vertical angles are always congruent. In this scenario, we have two known angles (42° and 55°) and an unknown angle x. However, angle x is vertical (and therefore congruent) to angle y. The equation can be set up based on the fact that the sum of angles on a straight line is 180°. Thus, we have: 42 + 55 + x = 180 |
Applications of Equations and Inequalities and Definition of an Angle |
|
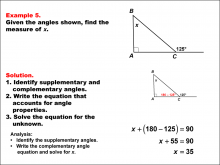
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 5 | Solving Equations Using Angle Properties: Example 5TopicEquations DescriptionThis example demonstrates solving equations using angle properties, specifically focusing on complementary angles and the exterior angle theorem. Complementary angles are two angles that sum to 90°, while the exterior angle theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. In this scenario, we have a right angle (90°), an exterior angle (125°), and an unknown angle x. Using the exterior angle theorem, we can set up the equation: x + 90 = 125. To solve for x, we subtract 90 from both sides: x = 35°. |
Applications of Equations and Inequalities and Definition of an Angle |

|
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 6 | Solving Equations Using Angle Properties: Example 6TopicEquations DescriptionThis example illustrates solving equations using angle properties, focusing on an isosceles right triangle. An isosceles right triangle has a right angle (90°) and two equal angles. In this scenario, we have the right angle given, and the two unknown equal angles represented by x. The equation can be set up based on the fact that the sum of angles in a triangle is 180°. Thus, we have: 90 + x + x = 180, or simplified, 90 + 2x = 180 To solve for x, we first subtract 90 from both sides: 2x = 90. Then, dividing both sides by 2, we get: x = 45°. |
Applications of Equations and Inequalities and Definition of an Angle |

|
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 7 | Solving Equations Using Angle Properties: Example 7TopicEquations DescriptionThis example demonstrates solving equations using angle properties, specifically focusing on parallel lines cut by a transversal and same side interior angles. When parallel lines are cut by a transversal, same side interior angles are supplementary, meaning they sum to 180°. In this scenario, we have one known angle of 112° and an unknown angle x. The 112° angle is vertical to the same side interior angle paired with x. The equation can be set up as: 112 + x = 180 |
Applications of Equations and Inequalities and Definition of an Angle |
|
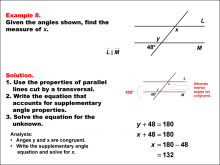
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 8 | Solving Equations Using Angle Properties: Example 8TopicEquations DescriptionThis example illustrates solving equations using angle properties, focusing on parallel lines cut by a transversal and alternate interior angles. When parallel lines are cut by a transversal, alternate interior angles are congruent, meaning they have the same measure. In this scenario, we have one known angle of 48° and an unknown angle x. Since x and y are alternate interior angles, they are congruent. We can now use the property of supplementary angles to solve for x: x + 48 = 180 x = 132° |
Applications of Equations and Inequalities and Definition of an Angle |
|
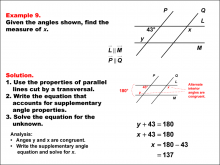
Math Example--Solving Equations--Solving Equations Using Angle Properties: Example 9 | Solving Equations Using Angle Properties: Example 9TopicEquations DescriptionThis example demonstrates solving equations using angle properties, specifically focusing on parallel lines cut by a transversal and alternate interior angles. When parallel lines are cut by a transversal, alternate interior angles are congruent, meaning they have the same measure. In this scenario, we have one known angle of 43° and an unknown angle x. However, angle x and angle y are alternate interior angles and are congruent. This means that x and teh 43° angle are same side interior angles, which are supplementary. We set up this equation: |
Definition of an Angle and Applications of Equations and Inequalities |
|
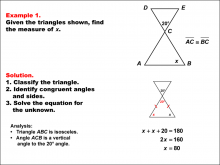
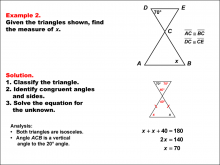
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 1 | Solving Equations Using Triangle Properties: Example 1TopicEquations DescriptionThis example focuses on solving equations using the properties of similar isosceles triangles. Isosceles triangles are characterized by having two equal sides and two equal base angles. In this case, we have two similar isosceles triangles, which means they share the same shape but may differ in size. The equation to be solved involves finding the unknown angle x, given that one of the angles is 20°. The property of vertical angles tells us that the angle vertical to the 20° angle is also 20° |
Applications of Equations and Inequalities and Applications of Triangles |
|
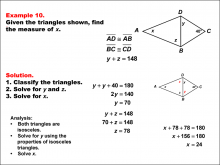
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 10 | Solving Equations Using Triangle Properties: Example 10TopicEquations DescriptionThis example, similar to Example 9, involves solving equations using the properties of a kite and applying the exterior angle theorem. We are again given one angle of 40° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 2 | Solving Equations Using Triangle Properties: Example 2TopicEquations DescriptionThis example explores solving equations using the properties of similar isosceles triangles, building upon the concepts introduced in Example 1. In this case, we have two similar isosceles triangles with one known angle of 70° and an unknown angle x. The goal is to determine the value of x using triangle properties and algebraic techniques. |
Applications of Equations and Inequalities and Applications of Triangles |
|
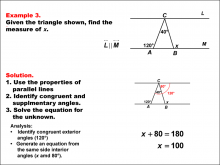
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 3 | Solving Equations Using Triangle Properties: Example 3TopicEquations DescriptionThis example focuses on solving equations involving parallel lines cut by a transversal, a fundamental concept in geometry. The problem presents two parallel lines intersected by two transversals that also form a triangle. We are given that one angle measures 120° and the corresponding angle can be expressed as (y + 40)°. The goal is to determine the value of y using the properties of angles formed by parallel lines and a transversal. When parallel lines are cut by a transversal, several important angle relationships are formed: |
Applications of Equations and Inequalities and Applications of Triangles |
|
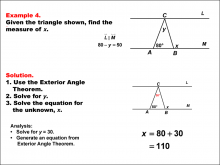
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4 | Solving Equations Using Triangle Properties: Example 4TopicEquations DescriptionThis example demonstrates solving equations using the Exterior Angle Theorem in the context of parallel lines cut by a transversal, two crucial concepts in geometry. The problem presents a triangle with two known interior angles of 80° and y, and an unknown exterior angle x°. We are also given that 80 - y = 50, which simplifies to y = 30. The goal is to determine the value of x using the properties of triangles and the Exterior Angle Theorem. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Wo we get x = 80 + 30, or x = 110. |
Applications of Equations and Inequalities and Applications of Triangles |
|
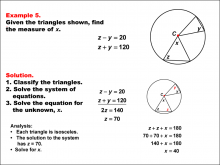
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 5 | Solving Equations Using Triangle Properties: Example 5TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles centered in a circle. The problem presents two equations: z - y = 20 and z + y = 120, where z and y represent angles in the isosceles triangles. The goal is to solve this system of equations to find the values of z and y, utilizing properties of isosceles triangles and circles. |
Applications of Equations and Inequalities and Applications of Triangles |
|
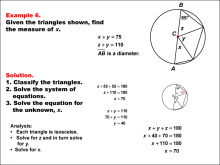
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 6 | Solving Equations Using Triangle Properties: Example 6TopicEquations DescriptionThis example explores solving equations involving triangles that share a vertex at the center of a circle. We are presented with two equations: x + y = 75 and z + y = 110, where x, y, and z represent angles in the triangle The goal is to solve this system of equations to find the values of x, y, and z, utilizing properties of isosceles triangles. Since each of the triangles is isosceles, we know that z + 55 + 55 = 180 and therefore, z = 70°. We substitute this into one of the equations: 70 + y = 110 7 = 40° |
Applications of Equations and Inequalities and Applications of Triangles |
|
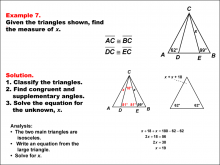
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 7 | Solving Equations Using Triangle Properties: Example 7TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles with a common vertex and base. We are given two angles, 62° and 99°, and need to find the unknown angle x. This problem demonstrates how to use the properties of isosceles triangles and the sum of angles in a triangle to solve for an unknown angle. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
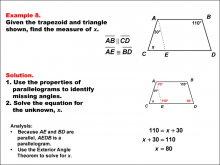
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 8 | Solving Equations Using Triangle Properties: Example 8TopicEquations DescriptionThis example involves solving an equation using the properties of a trapezoid with an embedded parallelogram and applying the exterior angle theorem. We are given two angles, 30° and 110°, and need to find the unknown angle x. This problem demonstrates the application of multiple geometric concepts to solve a complex equation. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
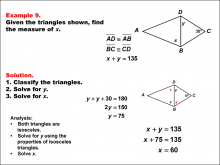
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 9 | Solving Equations Using Triangle Properties: Example 9TopicEquations DescriptionThis example focuses on solving equations using the properties of a kite and applying the exterior angle theorem. We are given one angle of 30° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 11 | Solving Equations with Angle Measures--Example 11TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12 | Solving Equations with Angle Measures--Example 12TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 13 | Solving Equations with Angle Measures--Example 13TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 14 | Solving Equations with Angle Measures--Example 14TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
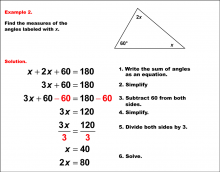
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 15 | Solving Equations with Angle Measures--Example 15TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 2 | Solving Equations with Angle Measures--Example 2TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3 | Solving Equations with Angle Measures--Example 3TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 4 | Solving Equations with Angle Measures--Example 4TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
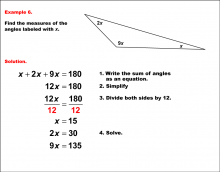
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 5 | Solving Equations with Angle Measures--Example 5TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 6 | Solving Equations with Angle Measures--Example 6TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 7 | Solving Equations with Angle Measures--Example 7TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 8 | Solving Equations with Angle Measures--Example 8TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9 | Solving Equations with Angle Measures--Example 9TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
|
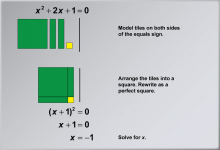
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 1 | Math Example: Solving Quadratic Equations with Algebra TilesTopicSolving Equations DescriptionIn this example, we explore solving the quadratic equation x2 + 2x + 1 = 0 using algebra tiles. The visual representation shows how to rearrange the equation into (x + 1)2 = 0, demonstrating the power of algebra tiles in simplifying complex equations. By arranging the tiles, students can physically see the relationship between the terms and understand how they combine to form a perfect square trinomial. |
Quadratic Equations and Functions |
|
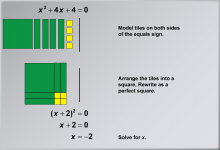
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 2 | Math Example: Solving Quadratic Equations with Algebra TilesTopicSolving Equations DescriptionThis example illustrates the process of solving the quadratic equation x2+ 4x + 4 = 0 using algebra tiles. The visual representation demonstrates how to rearrange the equation into (x + 2)2 = 0, showcasing the power of algebra tiles in simplifying and solving quadratic equations. By arranging the tiles, students can physically see how the terms combine to form a perfect square trinomial, making the solution process more intuitive. |
Quadratic Equations and Functions |
|
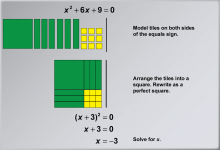
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 3 | Math Example: Solving Quadratic Equations with Algebra TilesTopicSolving Equations DescriptionThis example demonstrates the process of solving the quadratic equation x2 + 6x + 9 = 0 using algebra tiles. The visual representation shows how to rearrange the equation into (x + 3)2 = 0, illustrating the power of algebra tiles in simplifying and solving quadratic equations with larger coefficients. By arranging the tiles into a square, students can physically see how the terms combine to form a perfect square trinomial, making the solution process more intuitive and accessible. |
Quadratic Equations and Functions |
|
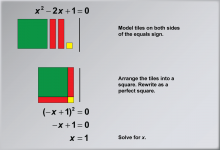
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 4 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 4TopicSolving Equations DescriptionIn this example, we explore solving the quadratic equation x2 - 2x + 1 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a perfect square, effectively transforming the equation into (-x + 1)2 = 0. This method showcases the versatility of algebra tiles in handling equations with both positive and negative terms, as well as illustrating the completing the square technique. |
Quadratic Equations and Functions |
|
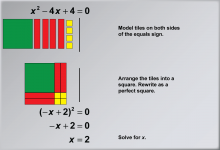
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 5 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 5TopicSolving Equations DescriptionThis example demonstrates the process of solving the quadratic equation x2 - 4x + 4 = 0 using algebra tiles. The visual representation shows how to arrange the tiles to form a perfect square, illustrating the completing the square method. By organizing the tiles, students can physically see how the terms combine to form the expression (-x + 2)2 = 0, making the solution process more intuitive and accessible. |
Quadratic Equations and Functions |
|
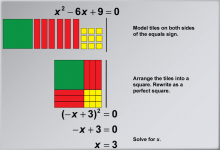
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 6 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 6TopicSolving Equations DescriptionThis example illustrates the process of solving the quadratic equation x2 - 6x + 9 = 0 using algebra tiles. By modeling tiles on both sides of the equation, students can visually understand the principle of maintaining equality while manipulating the equation. The tiles are arranged into a square to form a perfect square trinomial, demonstrating the completing the square method in a tangible way. |
Quadratic Equations and Functions |
|
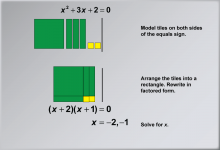
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 7 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 7TopicSolving Equations DescriptionThis example demonstrates the process of solving the quadratic equation x2 + 3x + 2 = 0 using algebra tiles. The visual representation shows how to arrange the tiles into a rectangle, illustrating the factoring method for solving quadratic equations. By organizing the tiles in this way, students can physically see how the terms combine to form the factored expression (x + 2)(x + 1) = 0, making the solution process more intuitive and accessible. |
Quadratic Equations and Functions |
|
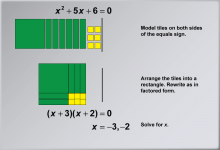
Math Example: Solving Quadratic Equations with Algebra Tiles--Example 8 | Math Example: Solving Quadratic Equations with Algebra Tiles--Example 8TopicSolving Equations DescriptionThis example illustrates the process of solving the quadratic equation x2 + 5x + 6 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a rectangle, showcasing the factoring method for solving quadratic equations. By organizing the tiles in this manner, students can physically see how the terms combine to form the factored expression (x + 3)(x + 2) = 0, making the solution process more concrete and understandable. |
Quadratic Equations and Functions |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 1 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 1TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition demonstrates solving the equation 2x + 3 = 7 by performing two inverse operations to isolate x. The operations shown are subtracting 3 from both sides and then dividing by 2. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 10 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 10TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition involves solving -3x + (-12) = -42 by performing two inverse operations: addition and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 2 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 2TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows solving the equation 3x + 4 = 13 by using two inverse operations. The steps involve subtracting 4 and then dividing by 3. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 3 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 3TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition involves solving the equation 2x + 4 = 8 using inverse operations. It shows subtraction and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 4 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 4TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition illustrates solving -4x + 5 = 25. It uses inverse operations by subtracting 5 and dividing by -4. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 5 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 5TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition shows the solution to -7x + 6 = 48 by isolating x with inverse operations, including subtraction and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 6 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 6TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition solves the equation 6x + (-2) = 34 by using inverse operations, specifically addition and division, to find the value of x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 7 | Math Example: Solving Two-Step Equations of the Form ax + b = c--Example 7TopicSolving Equations DescriptionAn example of solving a two-step equation involving multiplication and addition solves 10x + (-6) = 54 by isolating x through inverse operations, including addition and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution. Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations. |
Solving Two-Step Equations |