
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 5: Using Equations to Solve for Unknown Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
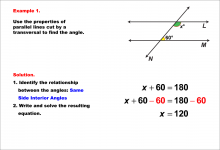
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 1 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 1TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
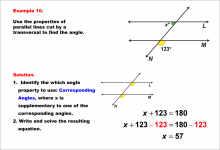
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 10 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 10TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
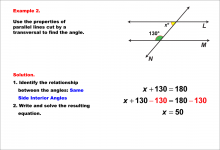
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 2 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 2TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
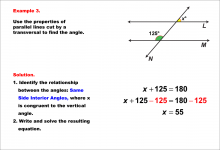
|
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 3 | TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
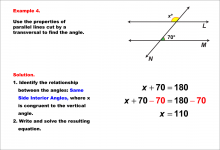
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 4 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 4TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
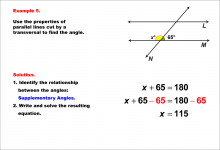
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 5 | TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
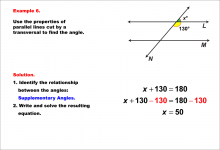
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 6 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 6TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
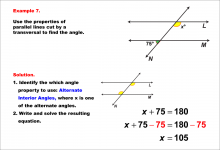
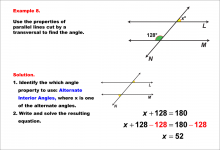
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 7 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 7TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
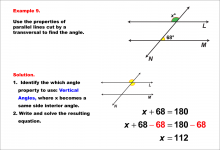
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 8 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 8TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
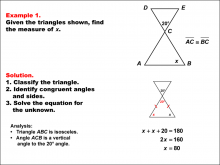
Math Example--Solving Equations--Equations with Angles from Parallel Lines Cut by a Transversal--Example 9 | Equations with Angles from Parallel Lines Cut by a Transversal--Example 9TopicEquations |
Parallel Lines, Applications of Angles and Planes and Applications of Equations and Inequalities |
|
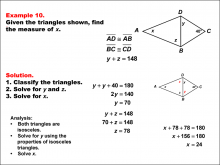
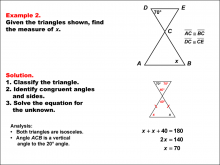
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 1 | Solving Equations Using Triangle Properties: Example 1TopicEquations DescriptionThis example focuses on solving equations using the properties of similar isosceles triangles. Isosceles triangles are characterized by having two equal sides and two equal base angles. In this case, we have two similar isosceles triangles, which means they share the same shape but may differ in size. The equation to be solved involves finding the unknown angle x, given that one of the angles is 20°. The property of vertical angles tells us that the angle vertical to the 20° angle is also 20° |
Applications of Equations and Inequalities and Applications of Triangles |
|
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 10 | Solving Equations Using Triangle Properties: Example 10TopicEquations DescriptionThis example, similar to Example 9, involves solving equations using the properties of a kite and applying the exterior angle theorem. We are again given one angle of 40° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 2 | Solving Equations Using Triangle Properties: Example 2TopicEquations DescriptionThis example explores solving equations using the properties of similar isosceles triangles, building upon the concepts introduced in Example 1. In this case, we have two similar isosceles triangles with one known angle of 70° and an unknown angle x. The goal is to determine the value of x using triangle properties and algebraic techniques. |
Applications of Equations and Inequalities and Applications of Triangles |
|
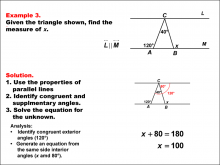
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 3 | Solving Equations Using Triangle Properties: Example 3TopicEquations DescriptionThis example focuses on solving equations involving parallel lines cut by a transversal, a fundamental concept in geometry. The problem presents two parallel lines intersected by two transversals that also form a triangle. We are given that one angle measures 120° and the corresponding angle can be expressed as (y + 40)°. The goal is to determine the value of y using the properties of angles formed by parallel lines and a transversal. When parallel lines are cut by a transversal, several important angle relationships are formed: |
Applications of Equations and Inequalities and Applications of Triangles |
|
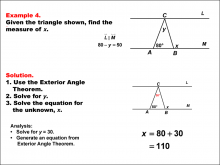
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 4 | Solving Equations Using Triangle Properties: Example 4TopicEquations DescriptionThis example demonstrates solving equations using the Exterior Angle Theorem in the context of parallel lines cut by a transversal, two crucial concepts in geometry. The problem presents a triangle with two known interior angles of 80° and y, and an unknown exterior angle x°. We are also given that 80 - y = 50, which simplifies to y = 30. The goal is to determine the value of x using the properties of triangles and the Exterior Angle Theorem. The Exterior Angle Theorem states that an exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. Wo we get x = 80 + 30, or x = 110. |
Applications of Equations and Inequalities and Applications of Triangles |
|
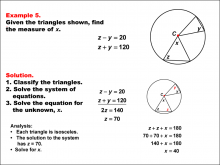
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 5 | Solving Equations Using Triangle Properties: Example 5TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles centered in a circle. The problem presents two equations: z - y = 20 and z + y = 120, where z and y represent angles in the isosceles triangles. The goal is to solve this system of equations to find the values of z and y, utilizing properties of isosceles triangles and circles. |
Applications of Equations and Inequalities and Applications of Triangles |
|
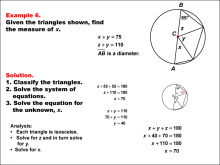
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 6 | Solving Equations Using Triangle Properties: Example 6TopicEquations DescriptionThis example explores solving equations involving triangles that share a vertex at the center of a circle. We are presented with two equations: x + y = 75 and z + y = 110, where x, y, and z represent angles in the triangle The goal is to solve this system of equations to find the values of x, y, and z, utilizing properties of isosceles triangles. Since each of the triangles is isosceles, we know that z + 55 + 55 = 180 and therefore, z = 70°. We substitute this into one of the equations: 70 + y = 110 7 = 40° |
Applications of Equations and Inequalities and Applications of Triangles |
|
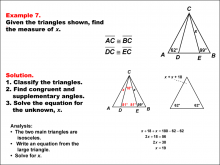
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 7 | Solving Equations Using Triangle Properties: Example 7TopicEquations DescriptionThis example focuses on solving equations involving isosceles triangles with a common vertex and base. We are given two angles, 62° and 99°, and need to find the unknown angle x. This problem demonstrates how to use the properties of isosceles triangles and the sum of angles in a triangle to solve for an unknown angle. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
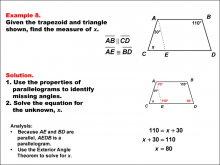
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 8 | Solving Equations Using Triangle Properties: Example 8TopicEquations DescriptionThis example involves solving an equation using the properties of a trapezoid with an embedded parallelogram and applying the exterior angle theorem. We are given two angles, 30° and 110°, and need to find the unknown angle x. This problem demonstrates the application of multiple geometric concepts to solve a complex equation. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
|
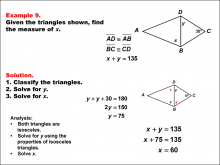
Math Example--Solving Equations--Solving Equations Using Triangle Properties: Example 9 | Solving Equations Using Triangle Properties: Example 9TopicEquations DescriptionThis example focuses on solving equations using the properties of a kite and applying the exterior angle theorem. We are given one angle of 30° and two unknown angles, y and x. The goal is to set up and solve equations to find the values of y and x using the properties of kites and the exterior angle theorem. Key properties to consider: |
Applications of Equations and Inequalities and Applications of Triangles |
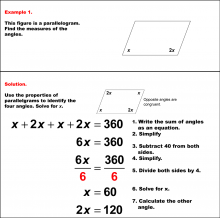
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 1 | Solving Equations with Angle Measures 2--Example 1TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 10 | Solving Equations with Angle Measures 2--Example 10TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
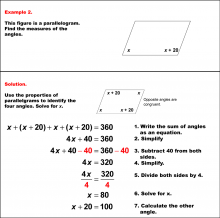
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 2 | Solving Equations with Angle Measures 2--Example 2TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
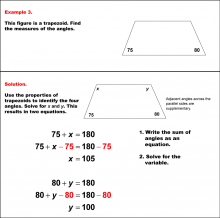
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 3 | Solving Equations with Angle Measures 2--Example 3TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
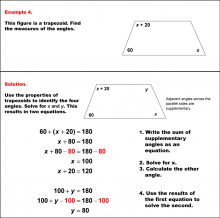
|
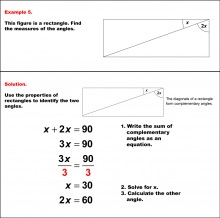
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 4 | Solving Equations with Angle Measures 2--Example 4TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 5 | Solving Equations with Angle Measures 2--Example 5TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
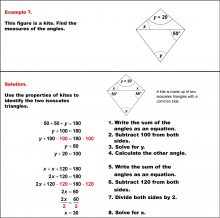
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 6 | Solving Equations with Angle Measures 2--Example 6TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |
|
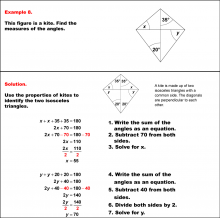
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 7 | Solving Equations with Angle Measures 2--Example 7TopicEquations DescriptionThis example demonstrates solving equations involving angle measures in a kite. A kite has two pairs of adjacent congruent angles. In this case, we have angles represented as (x+50)°, (x+50)°, (y+20)°, and y°. To solve this problem, we apply two key principles: the sum of angles in a quadrilateral is 360°, and the sum of the angles of a triangle is 180°. You can use the triangle equation to solve for y. Once you determine the value for y, you can use that to find x using either the triangle or the quadrilateral equation. In the solution shown, the triangle equation is used. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
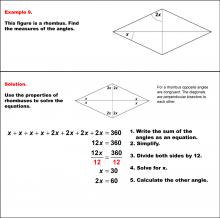
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 8 | Solving Equations with Angle Measures 2--Example 8TopicEquations DescriptionThis example illustrates solving equations involving angle measures in a kite. The kite has two known angles of 70° and 40°, and two unknown angles represented as (x+y)°. To solve this problem, we look at the triangles formed by one of the diagonals of the kite and use the triangle equation. First solve for x with the top triangle. Once you find x, use that value to solve for y in the bottom triangle. You could also use the quadrilateral equation to solve for y. |
Solving Multistep Equations and Applications of Quadrilaterals |
|
Math Example--Solving Equations--Solving Equations with Angle Measures 2--Example 9 | Solving Equations with Angle Measures 2--Example 9TopicEquations |
Solving Multistep Equations and Applications of Quadrilaterals |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 1 | Solving Equations with Angle Measures--Example 1TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 10 | Solving Equations with Angle Measures--Example 10TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 11 | Solving Equations with Angle Measures--Example 11TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 12 | Solving Equations with Angle Measures--Example 12TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 13 | Solving Equations with Angle Measures--Example 13TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 14 | Solving Equations with Angle Measures--Example 14TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 15 | Solving Equations with Angle Measures--Example 15TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
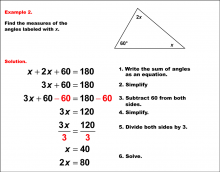
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 2 | Solving Equations with Angle Measures--Example 2TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 3 | Solving Equations with Angle Measures--Example 3TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 4 | Solving Equations with Angle Measures--Example 4TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 5 | Solving Equations with Angle Measures--Example 5TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |
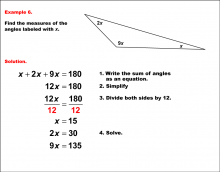
|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 6 | Solving Equations with Angle Measures--Example 6TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 7 | Solving Equations with Angle Measures--Example 7TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 8 | Solving Equations with Angle Measures--Example 8TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |

|
Math Example--Solving Equations--Solving Equations with Angle Measures--Example 9 | Solving Equations with Angle Measures--Example 9TopicEquations |
Solving Multistep Equations and Applications of Angles and Planes |